A machine learning approach for efficient multi-dimensional integration
Paper and Code
Sep 14, 2020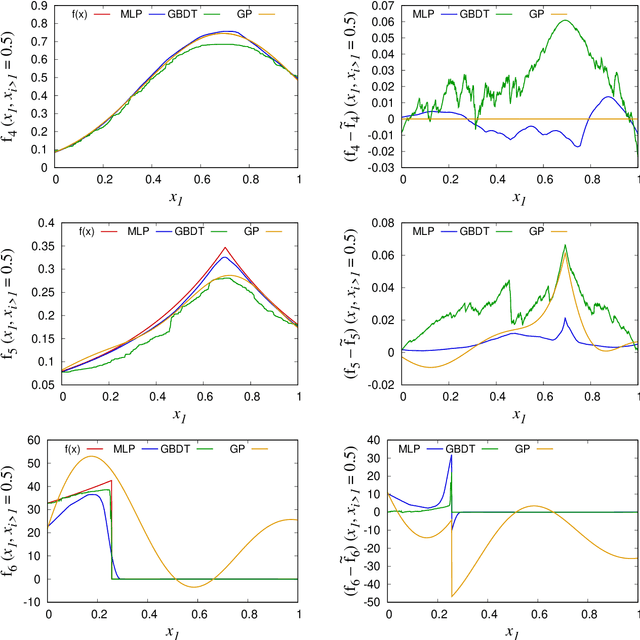

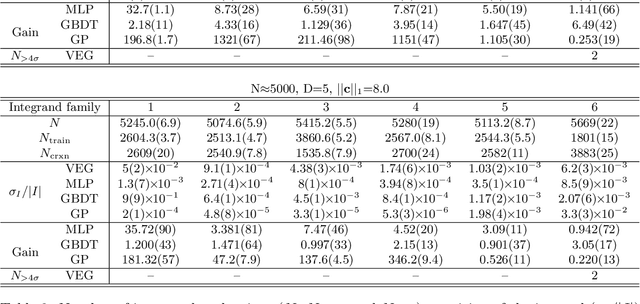

We propose a novel multi-dimensional integration algorithm using a machine learning (ML) technique. After training a ML regression model to mimic a target integrand, the regression model is used to evaluate an approximation of the integral. Then, the difference between the approximation and the true answer is calculated to correct the bias in the approximation of the integral induced by a ML prediction error. Because of the bias correction, the final estimate of the integral is unbiased and has a statistically correct error estimation. The performance of the proposed algorithm is demonstrated on six different types of integrands at various dimensions and integrand difficulties. The results show that, for the same total number of integrand evaluations, the new algorithm provides integral estimates with more than an order of magnitude smaller uncertainties than those of the VEGAS algorithm in most of the test cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge