Less is More! A slim architecture for optimal language translation

The softmax attention mechanism has emerged as a noteworthy development in the field of Artificial Intelligence research, building on the successes of Transformer-based architectures. However, their ever increasing sizes necessitate ever increasing computational memory, that limits their usage. We propose KgV, a sigmoid gating mechanism that, in conjunction with softmax attention, significantly boosts performance without increasing architecture size. To amend the size requirements, we leverage Tensor Chains to identify and prune the excess parameters. We find that such excess resides primarily within the embedding layer, and not in the output linear layer. To further improve embedding and significantly reduce parameters, we introduce H-SoftPOS, a hierarchical embedding layer which simultaneously enhances performance. Remarkably, on the WMT14 English-German validation set, our approach yields a threefold reduction in perplexity, surpassing the current state-of-the-art, while reducing parameter counts also by a factor of 3. When we further reduce the number of parameters up to sevenfold, we can still achieve a 21\% decrease in perplexity with respect to the baseline Transformer. To understand generalization capabilities, we conduct experiments on the 7 language pairs of the WMT17 dataset. Our method outperforms existing techniques in terms of test loss while simultaneously halving the number of parameters. Moreover, we observe a 70 times reduction in variance with respect to the prior state-of-the-art. In conclusion, our proposed method yields significant improvements in performance and much lower memory cost. We call the resulting architecture Anthe.

Prediction and compression of lattice QCD data using machine learning algorithms on quantum annealer

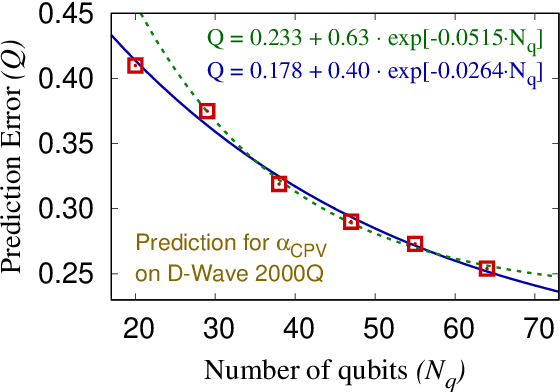
We present regression and compression algorithms for lattice QCD data utilizing the efficient binary optimization ability of quantum annealers. In the regression algorithm, we encode the correlation between the input and output variables into a sparse coding machine learning algorithm. The trained correlation pattern is used to predict lattice QCD observables of unseen lattice configurations from other observables measured on the lattice. In the compression algorithm, we define a mapping from lattice QCD data of floating-point numbers to the binary coefficients that closely reconstruct the input data from a set of basis vectors. Since the reconstruction is not exact, the mapping defines a lossy compression, but, a reasonably small number of binary coefficients are able to reconstruct the input vector of lattice QCD data with the reconstruction error much smaller than the statistical fluctuation. In both applications, we use D-Wave quantum annealers to solve the NP-hard binary optimization problems of the machine learning algorithms.

Lossy compression of statistical data using quantum annealer

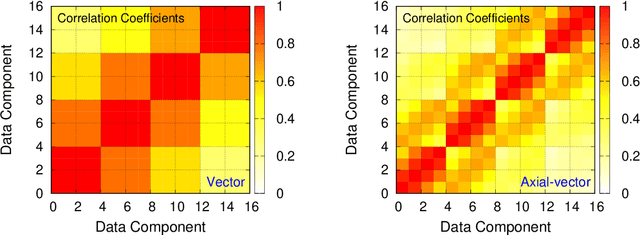
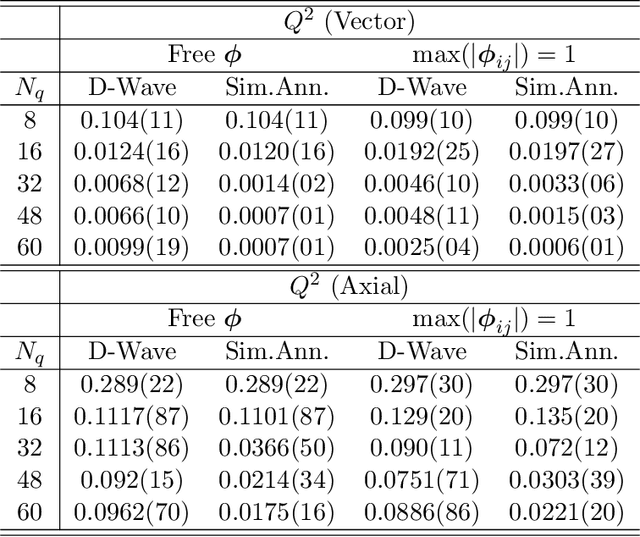
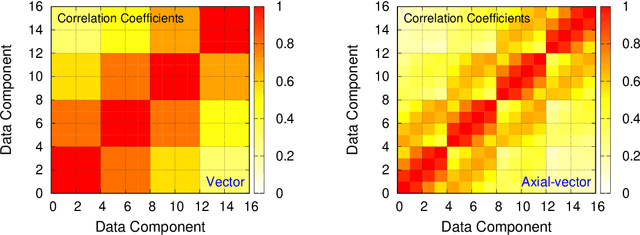
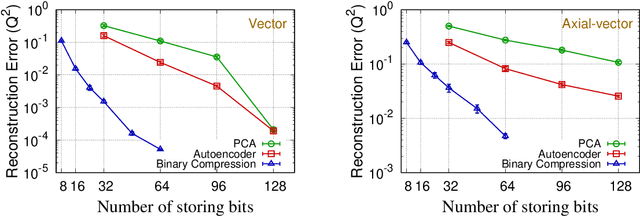
We present a new lossy compression algorithm for statistical floating-point data through a representation learning with binary variables. The algorithm finds a set of basis vectors and their binary coefficients that precisely reconstruct the original data. The optimization for the basis vectors is performed classically, while binary coefficients are retrieved through both simulated and quantum annealing for comparison. A bias correction procedure is also presented to estimate and eliminate the error and bias introduced from the inexact reconstruction of the lossy compression for statistical data analyses. The compression algorithm is demonstrated on two different datasets of lattice quantum chromodynamics simulations. The results obtained using simulated annealing show 3.5 times better compression performance than the algorithms based on a neural-network autoencoder and principal component analysis. Calculations using quantum annealing also show promising results, but performance is limited by the integrated control error of the quantum processing unit, which yields large uncertainties in the biases and coupling parameters. Hardware comparison is further studied between the previous generation D-Wave 2000Q and the current D-Wave Advantage system. Our study shows that the Advantage system is more likely to obtain low-energy solutions for the problems than the 2000Q.