Nathan McDonald
A Practical Guide to Tuning Spiking Neuronal Dynamics
Jun 09, 2025Abstract:In this work, we examine fundamental elements of spiking neural networks (SNNs) as well as how to tune them. Concretely, we focus on two different foundational neuronal units utilized in SNNs -- the leaky integrate-and-fire (LIF) and the resonate-and-fire (RAF) neuron. We explore key equations and how hyperparameter values affect behavior. Beyond hyperparameters, we discuss other important design elements of SNNs -- the choice of input encoding and the setup for excitatory-inhibitory populations -- and how these impact LIF and RAF dynamics.
Assembling Modular, Hierarchical Cognitive Map Learners with Hyperdimensional Computing
Apr 29, 2024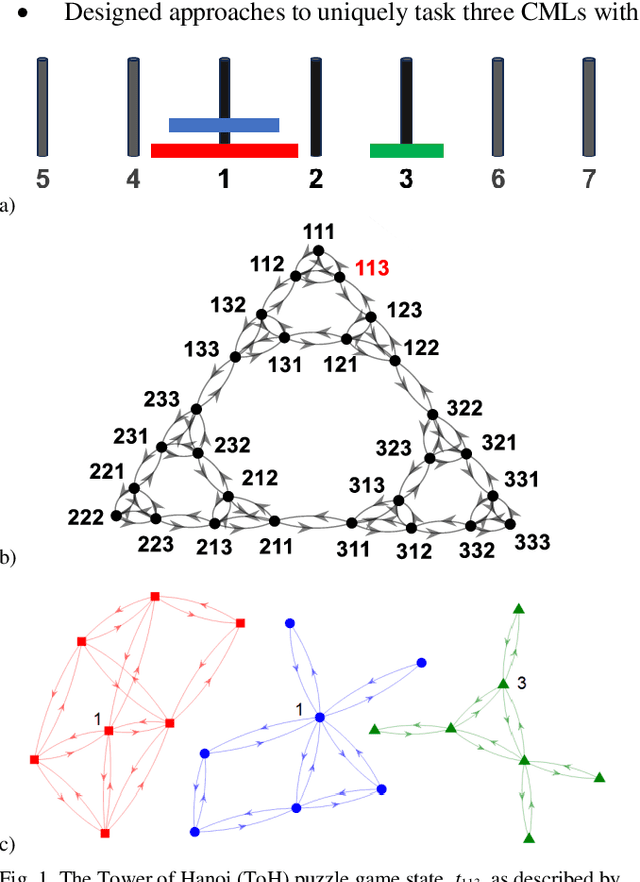
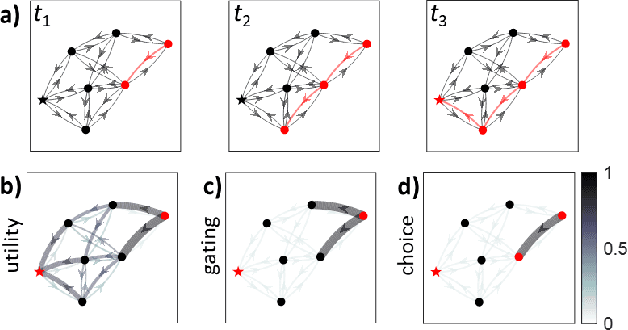
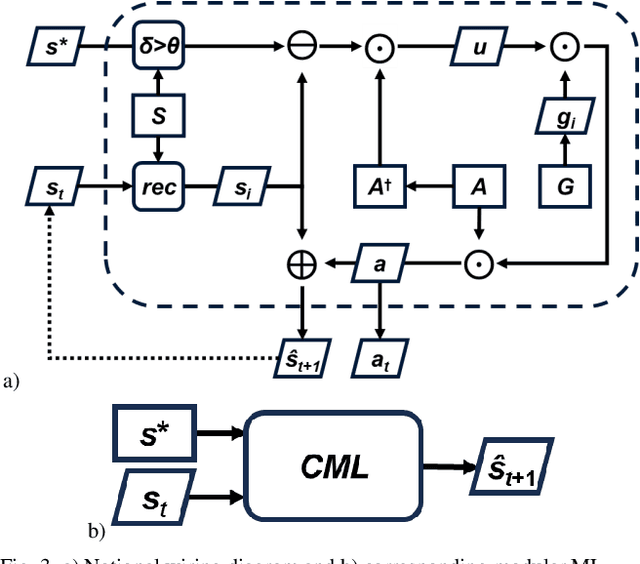
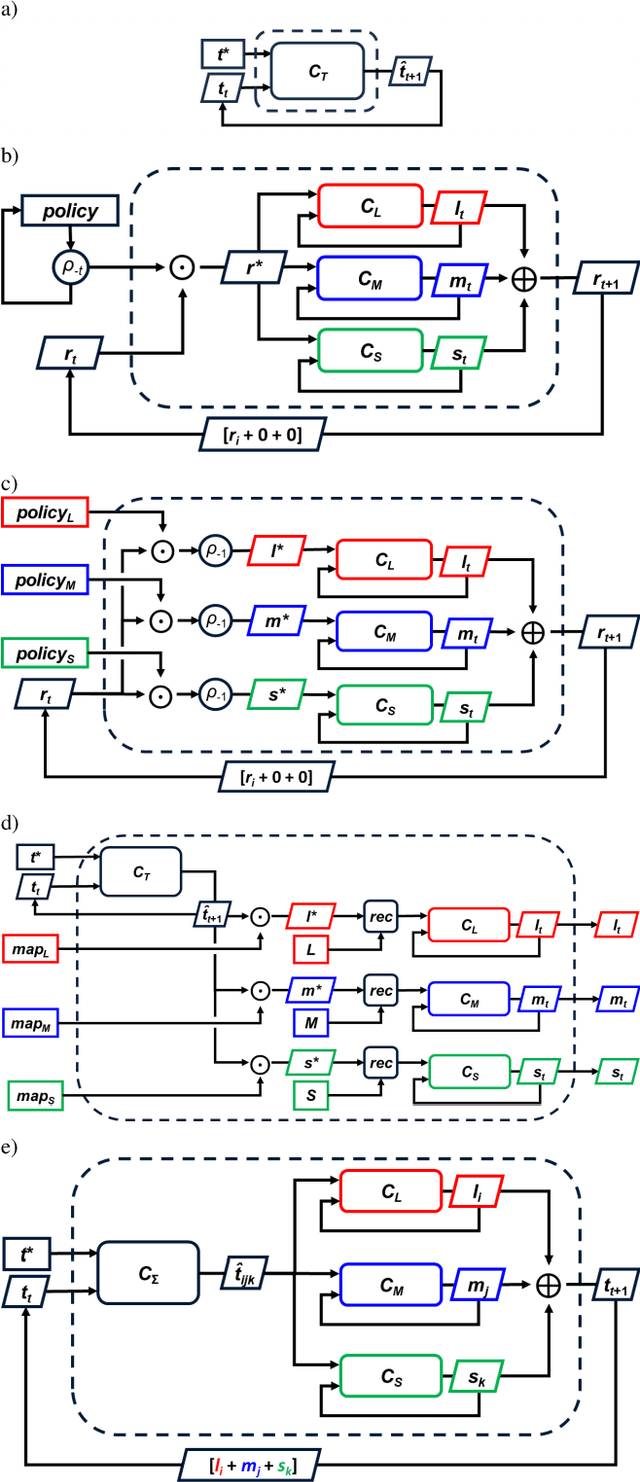
Abstract:Cognitive map learners (CML) are a collection of separate yet collaboratively trained single-layer artificial neural networks (matrices), which navigate an abstract graph by learning internal representations of the node states, edge actions, and edge action availabilities. A consequence of this atypical segregation of information is that the CML performs near-optimal path planning between any two graph node states. However, the CML does not learn when or why to transition from one node to another. This work created CMLs with node states expressed as high dimensional vectors consistent with hyperdimensional computing (HDC), a form of symbolic machine learning (ML). This work evaluated HDC-based CMLs as ML modules, capable of receiving external inputs and computing output responses which are semantically meaningful for other HDC-based modules. Several CMLs were prepared independently then repurposed to solve the Tower of Hanoi puzzle without retraining these CMLs and without explicit reference to their respective graph topologies. This work suggests a template for building levels of biologically plausible cognitive abstraction and orchestration.
Modular, Hierarchical Machine Learning for Sequential Goal Completion
Apr 29, 2024Abstract:Given a maze populated with different objects, one may task a robot with a sequential goal completion task, e.g. 1) pick up a key then 2) unlock the door then 3) unlock the treasure chest. A typical machine learning (ML) solution would involve a monolithically trained artificial neural network (ANN). However, if the sequence of goals or the goals themselves change, then the ANN must be significantly (or, at worst, completely) retrained. Instead of a monolithic ANN, a modular ML component would be 1) independently optimizable (task-agnostic) and 2) arbitrarily reconfigurable with other ML modules. This work describes a modular, hierarchical ML framework by integrating two emerging ML techniques: 1) cognitive map learners (CML) and 2) hyperdimensional computing (HDC). A CML is a collection of three single layer ANNs (matrices) collaboratively trained to learn the topology of an abstract graph. Here, two CMLs were constructed, one describing locations on in 2D physical space and the other the relative distribution of objects found in this space. Each CML node states was encoded as a high-dimensional vector to utilize HDC, an ML algebra, for symbolic reasoning over these high-dimensional symbol vectors. In this way, each sub-goal above was described by algebraic equations of CML node states. Multiple, independently trained CMLs were subsequently assembled together to navigate a maze to solve a sequential goal task. Critically, changes to these goals required only localized changes in the CML-HDC architecture, as opposed to a global ANN retraining scheme. This framework therefore enabled a more traditional engineering approach to ML, akin to digital logic design.
Modularizing and Assembling Cognitive Map Learners via Hyperdimensional Computing
Apr 10, 2023Abstract:Biological organisms must learn how to control their own bodies to achieve deliberate locomotion, that is, predict their next body position based on their current position and selected action. Such learning is goal-agnostic with respect to maximizing (minimizing) an environmental reward (penalty) signal. A cognitive map learner (CML) is a collection of three separate yet collaboratively trained artificial neural networks which learn to construct representations for the node states and edge actions of an arbitrary bidirectional graph. In so doing, a CML learns how to traverse the graph nodes; however, the CML does not learn when and why to move from one node state to another. This work created CMLs with node states expressed as high dimensional vectors suitable for hyperdimensional computing (HDC), a form of symbolic machine learning (ML). In so doing, graph knowledge (CML) was segregated from target node selection (HDC), allowing each ML approach to be trained independently. The first approach used HDC to engineer an arbitrary number of hierarchical CMLs, where each graph node state specified target node states for the next lower level CMLs to traverse to. Second, an HDC-based stimulus-response experience model was demonstrated per CML. Because hypervectors may be in superposition with each other, multiple experience models were added together and run in parallel without any retraining. Lastly, a CML-HDC ML unit was modularized: trained with proxy symbols such that arbitrary, application-specific stimulus symbols could be operated upon without retraining either CML or HDC model. These methods provide a template for engineering heterogenous ML systems.
An FPGA Implementation of a Time Delay Reservoir Using Stochastic Logic
Sep 12, 2018



Abstract:This paper presents and demonstrates a stochastic logic time delay reservoir design in FPGA hardware. The reservoir network approach is analyzed using a number of metrics, such as kernel quality, generalization rank, performance on simple benchmarks, and is also compared to a deterministic design. A novel re-seeding method is introduced to reduce the adverse effects of stochastic noise, which may also be implemented in other stochastic logic reservoir computing designs, such as echo state networks. Benchmark results indicate that the proposed design performs well on noise-tolerant classification problems, but more work needs to be done to improve the stochastic logic time delay reservoirs robustness for regression problems. In addition, we show that the stochastic design can significantly reduce area cost if the conversion between binary and stochastic representations implemented efficiently.
Reservoir Computing and Extreme Learning Machines using Pairs of Cellular Automata Rules
Mar 16, 2017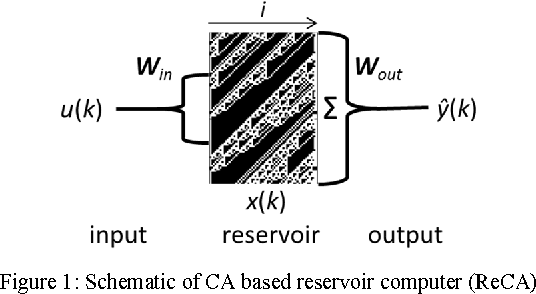

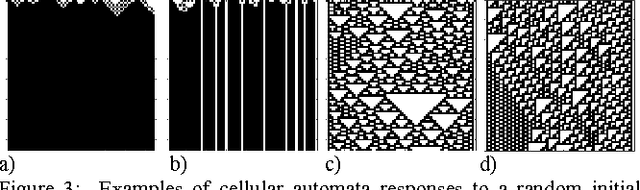
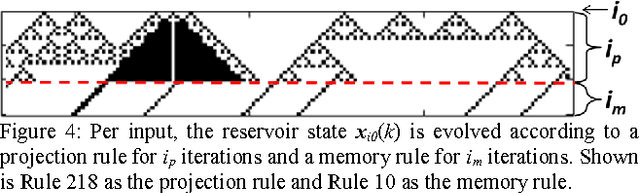
Abstract:A framework for implementing reservoir computing (RC) and extreme learning machines (ELMs), two types of artificial neural networks, based on 1D elementary Cellular Automata (CA) is presented, in which two separate CA rules explicitly implement the minimum computational requirements of the reservoir layer: hyperdimensional projection and short-term memory. CAs are cell-based state machines, which evolve in time in accordance with local rules based on a cells current state and those of its neighbors. Notably, simple single cell shift rules as the memory rule in a fixed edge CA afforded reasonable success in conjunction with a variety of projection rules, potentially significantly reducing the optimal solution search space. Optimal iteration counts for the CA rule pairs can be estimated for some tasks based upon the category of the projection rule. Initial results support future hardware realization, where CAs potentially afford orders of magnitude reduction in size, weight, and power (SWaP) requirements compared with floating point RC implementations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge