LatticeVision: Image to Image Networks for Modeling Non-Stationary Spatial Data

In many scientific and industrial applications, we are given a handful of instances (a 'small ensemble') of a spatially distributed quantity (a 'field') but would like to acquire many more. For example, a large ensemble of global temperature sensitivity fields from a climate model can help farmers, insurers, and governments plan appropriately. When acquiring more data is prohibitively expensive -- as is the case with climate models -- statistical emulation offers an efficient alternative for simulating synthetic yet realistic fields. However, parameter inference using maximum likelihood estimation (MLE) is computationally prohibitive, especially for large, non-stationary fields. Thus, many recent works train neural networks to estimate parameters given spatial fields as input, sidestepping MLE completely. In this work we focus on a popular class of parametric, spatially autoregressive (SAR) models. We make a simple yet impactful observation; because the SAR parameters can be arranged on a regular grid, both inputs (spatial fields) and outputs (model parameters) can be viewed as images. Using this insight, we demonstrate that image-to-image (I2I) networks enable faster and more accurate parameter estimation for a class of non-stationary SAR models with unprecedented complexity.

Wasserstein Distributional Learning

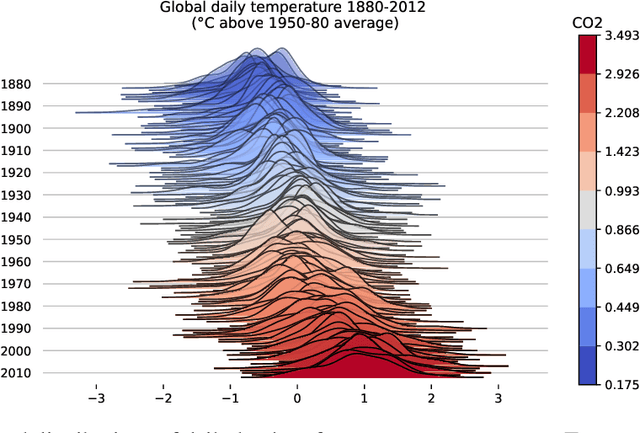
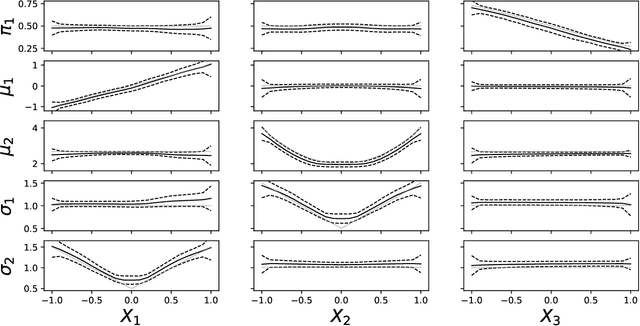
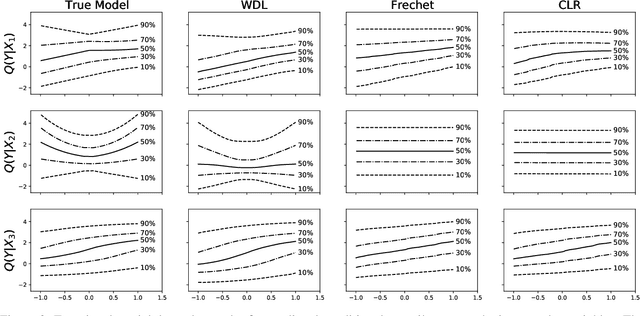
Learning conditional densities and identifying factors that influence the entire distribution are vital tasks in data-driven applications. Conventional approaches work mostly with summary statistics, and are hence inadequate for a comprehensive investigation. Recently, there have been developments on functional regression methods to model density curves as functional outcomes. A major challenge for developing such models lies in the inherent constraint of non-negativity and unit integral for the functional space of density outcomes. To overcome this fundamental issue, we propose Wasserstein Distributional Learning (WDL), a flexible density-on-scalar regression modeling framework that starts with the Wasserstein distance $W_2$ as a proper metric for the space of density outcomes. We then introduce a heterogeneous and flexible class of Semi-parametric Conditional Gaussian Mixture Models (SCGMM) as the model class $\mathfrak{F} \otimes \mathcal{T}$. The resulting metric space $(\mathfrak{F} \otimes \mathcal{T}, W_2)$ satisfies the required constraints and offers a dense and closed functional subspace. For fitting the proposed model, we further develop an efficient algorithm based on Majorization-Minimization optimization with boosted trees. Compared with methods in the previous literature, WDL better characterizes and uncovers the nonlinear dependence of the conditional densities, and their derived summary statistics. We demonstrate the effectiveness of the WDL framework through simulations and real-world applications.