Natalie Lang
Adaptive Deadline and Batch Layered Synchronized Federated Learning
May 29, 2025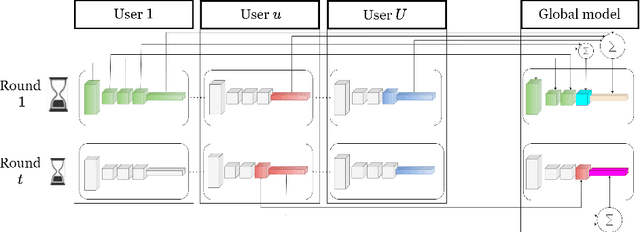
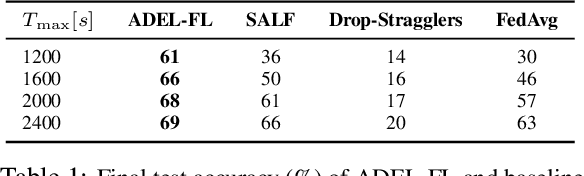
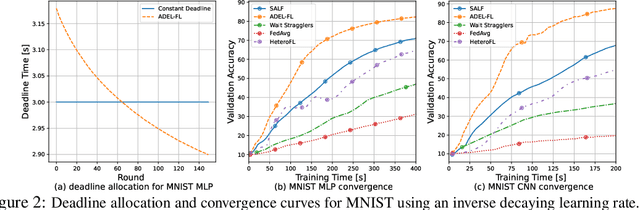
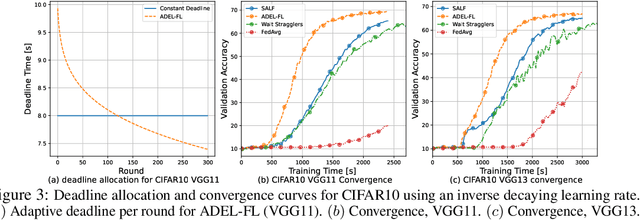
Abstract:Federated learning (FL) enables collaborative model training across distributed edge devices while preserving data privacy, and typically operates in a round-based synchronous manner. However, synchronous FL suffers from latency bottlenecks due to device heterogeneity, where slower clients (stragglers) delay or degrade global updates. Prior solutions, such as fixed deadlines, client selection, and layer-wise partial aggregation, alleviate the effect of stragglers, but treat round timing and local workload as static parameters, limiting their effectiveness under strict time constraints. We propose ADEL-FL, a novel framework that jointly optimizes per-round deadlines and user-specific batch sizes for layer-wise aggregation. Our approach formulates a constrained optimization problem minimizing the expected L2 distance to the global optimum under total training time and global rounds. We provide a convergence analysis under exponential compute models and prove that ADEL-FL yields unbiased updates with bounded variance. Extensive experiments demonstrate that ADEL-FL outperforms alternative methods in both convergence rate and final accuracy under heterogeneous conditions.
Memory-Efficient Distributed Unlearning
May 06, 2025Abstract:Machine unlearning considers the removal of the contribution of a set of data points from a trained model. In a distributed setting, where a server orchestrates training using data available at a set of remote users, unlearning is essential to cope with late-detected malicious or corrupted users. Existing distributed unlearning algorithms require the server to store all model updates observed in training, leading to immense storage overhead for preserving the ability to unlearn. In this work we study lossy compression schemes for facilitating distributed server-side unlearning with limited memory footprint. We propose memory-efficient distributed unlearning (MEDU), a hierarchical lossy compression scheme tailored for server-side unlearning, that integrates user sparsification, differential thresholding, and random lattice coding, to substantially reduce memory footprint. We rigorously analyze MEDU, deriving an upper bound on the difference between the desired model that is trained from scratch and the model unlearned from lossy compressed stored updates. Our bound outperforms the state-of-the-art known bounds for non-compressed decentralized server-side unlearning, even when lossy compression is incorporated. We further provide a numerical study, which shows that suited lossy compression can enable distributed unlearning with notably reduced memory footprint at the server while preserving the utility of the unlearned model.
PAUSE: Low-Latency and Privacy-Aware Active User Selection for Federated Learning
Mar 17, 2025Abstract:Federated learning (FL) enables multiple edge devices to collaboratively train a machine learning model without the need to share potentially private data. Federated learning proceeds through iterative exchanges of model updates, which pose two key challenges: First, the accumulation of privacy leakage over time, and second, communication latency. These two limitations are typically addressed separately: The former via perturbed updates to enhance privacy and the latter using user selection to mitigate latency - both at the expense of accuracy. In this work, we propose a method that jointly addresses the accumulation of privacy leakage and communication latency via active user selection, aiming to improve the trade-off among privacy, latency, and model performance. To achieve this, we construct a reward function that accounts for these three objectives. Building on this reward, we propose a multi-armed bandit (MAB)-based algorithm, termed Privacy-aware Active User SElection (PAUSE) which dynamically selects a subset of users each round while ensuring bounded overall privacy leakage. We establish a theoretical analysis, systematically showing that the reward growth rate of PAUSE follows that of the best-known rate in MAB literature. To address the complexity overhead of active user selection, we propose a simulated annealing-based relaxation of PAUSE and analyze its ability to approximate the reward-maximizing policy under reduced complexity. We numerically validate the privacy leakage, associated improved latency, and accuracy gains of our methods for the federated training in various scenarios.
Stragglers-Aware Low-Latency Synchronous Federated Learning via Layer-Wise Model Updates
Mar 27, 2024Abstract:Synchronous federated learning (FL) is a popular paradigm for collaborative edge learning. It typically involves a set of heterogeneous devices locally training neural network (NN) models in parallel with periodic centralized aggregations. As some of the devices may have limited computational resources and varying availability, FL latency is highly sensitive to stragglers. Conventional approaches discard incomplete intra-model updates done by stragglers, alter the amount of local workload and architecture, or resort to asynchronous settings; which all affect the trained model performance under tight training latency constraints. In this work, we propose straggler-aware layer-wise federated learning (SALF) that leverages the optimization procedure of NNs via backpropagation to update the global model in a layer-wise fashion. SALF allows stragglers to synchronously convey partial gradients, having each layer of the global model be updated independently with a different contributing set of users. We provide a theoretical analysis, establishing convergence guarantees for the global model under mild assumptions on the distribution of the participating devices, revealing that SALF converges at the same asymptotic rate as FL with no timing limitations. This insight is matched with empirical observations, demonstrating the performance gains of SALF compared to alternative mechanisms mitigating the device heterogeneity gap in FL.
Joint Privacy Enhancement and Quantization in Federated Learning
Aug 23, 2022



Abstract:Federated learning (FL) is an emerging paradigm for training machine learning models using possibly private data available at edge devices. The distributed operation of FL gives rise to challenges that are not encountered in centralized machine learning, including the need to preserve the privacy of the local datasets, and the communication load due to the repeated exchange of updated models. These challenges are often tackled individually via techniques that induce some distortion on the updated models, e.g., local differential privacy (LDP) mechanisms and lossy compression. In this work we propose a method coined joint privacy enhancement and quantization (JoPEQ), which jointly implements lossy compression and privacy enhancement in FL settings. In particular, JoPEQ utilizes vector quantization based on random lattice, a universal compression technique whose byproduct distortion is statistically equivalent to additive noise. This distortion is leveraged to enhance privacy by augmenting the model updates with dedicated multivariate privacy preserving noise. We show that JoPEQ simultaneously quantizes data according to a required bit-rate while holding a desired privacy level, without notably affecting the utility of the learned model. This is shown via analytical LDP guarantees, distortion and convergence bounds derivation, and numerical studies. Finally, we empirically assert that JoPEQ demolishes common attacks known to exploit privacy leakage.
DeepUME: Learning the Universal Manifold Embedding for Robust Point Cloud Registration
Dec 18, 2021



Abstract:Registration of point clouds related by rigid transformations is one of the fundamental problems in computer vision. However, a solution to the practical scenario of aligning sparsely and differently sampled observations in the presence of noise is still lacking. We approach registration in this scenario with a fusion of the closed-form Universal Mani-fold Embedding (UME) method and a deep neural network. The two are combined into a single unified framework, named DeepUME, trained end-to-end and in an unsupervised manner. To successfully provide a global solution in the presence of large transformations, we employ an SO(3)-invariant coordinate system to learn both a joint-resampling strategy of the point clouds and SO(3)-invariant features. These features are then utilized by the geometric UME method for transformation estimation. The parameters of DeepUME are optimized using a metric designed to overcome an ambiguity problem emerging in the registration of symmetric shapes, when noisy scenarios are considered. We show that our hybrid method outperforms state-of-the-art registration methods in various scenarios, and generalizes well to unseen data sets. Our code is publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge