Narayana Santhanam
On Modeling Profiles instead of Values
Jul 11, 2012
Abstract:We consider the problem of estimating the distribution underlying an observed sample of data. Instead of maximum likelihood, which maximizes the probability of the ob served values, we propose a different estimate, the high-profile distribution, which maximizes the probability of the observed profile the number of symbols appearing any given number of times. We determine the high-profile distribution of several data samples, establish some of its general properties, and show that when the number of distinct symbols observed is small compared to the data size, the high-profile and maximum-likelihood distributions are roughly the same, but when the number of symbols is large, the distributions differ, and high-profile better explains the data.
Information-theoretic limits of selecting binary graphical models in high dimensions
May 16, 2009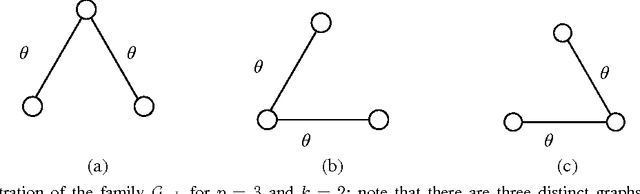
Abstract:The problem of graphical model selection is to correctly estimate the graph structure of a Markov random field given samples from the underlying distribution. We analyze the information-theoretic limitations of the problem of graph selection for binary Markov random fields under high-dimensional scaling, in which the graph size $p$ and the number of edges $k$, and/or the maximal node degree $d$ are allowed to increase to infinity as a function of the sample size $n$. For pairwise binary Markov random fields, we derive both necessary and sufficient conditions for correct graph selection over the class $\mathcal{G}_{p,k}$ of graphs on $p$ vertices with at most $k$ edges, and over the class $\mathcal{G}_{p,d}$ of graphs on $p$ vertices with maximum degree at most $d$. For the class $\mathcal{G}_{p, k}$, we establish the existence of constants $c$ and $c'$ such that if $\numobs < c k \log p$, any method has error probability at least 1/2 uniformly over the family, and we demonstrate a graph decoder that succeeds with high probability uniformly over the family for sample sizes $\numobs > c' k^2 \log p$. Similarly, for the class $\mathcal{G}_{p,d}$, we exhibit constants $c$ and $c'$ such that for $n < c d^2 \log p$, any method fails with probability at least 1/2, and we demonstrate a graph decoder that succeeds with high probability for $n > c' d^3 \log p$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge