Alon Orlitsky
Linear Regression using Heterogeneous Data Batches
Sep 05, 2023


Abstract:In many learning applications, data are collected from multiple sources, each providing a \emph{batch} of samples that by itself is insufficient to learn its input-output relationship. A common approach assumes that the sources fall in one of several unknown subgroups, each with an unknown input distribution and input-output relationship. We consider one of this setup's most fundamental and important manifestations where the output is a noisy linear combination of the inputs, and there are $k$ subgroups, each with its own regression vector. Prior work~\cite{kong2020meta} showed that with abundant small-batches, the regression vectors can be learned with only few, $\tilde\Omega( k^{3/2})$, batches of medium-size with $\tilde\Omega(\sqrt k)$ samples each. However, the paper requires that the input distribution for all $k$ subgroups be isotropic Gaussian, and states that removing this assumption is an ``interesting and challenging problem". We propose a novel gradient-based algorithm that improves on the existing results in several ways. It extends the applicability of the algorithm by: (1) allowing the subgroups' underlying input distributions to be different, unknown, and heavy-tailed; (2) recovering all subgroups followed by a significant proportion of batches even for infinite $k$; (3) removing the separation requirement between the regression vectors; (4) reducing the number of batches and allowing smaller batch sizes.
TURF: A Two-factor, Universal, Robust, Fast Distribution Learning Algorithm
Feb 15, 2022
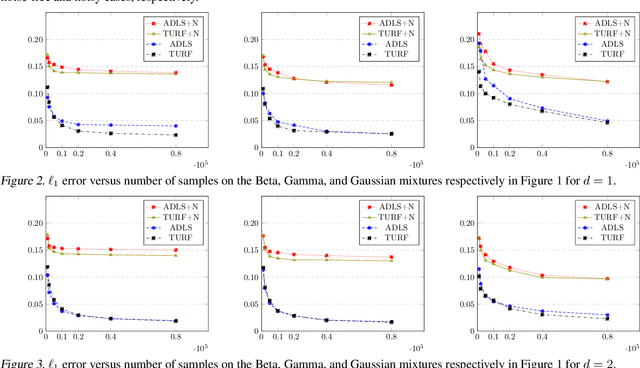
Abstract:Approximating distributions from their samples is a canonical statistical-learning problem. One of its most powerful and successful modalities approximates every distribution to an $\ell_1$ distance essentially at most a constant times larger than its closest $t$-piece degree-$d$ polynomial, where $t\ge1$ and $d\ge0$. Letting $c_{t,d}$ denote the smallest such factor, clearly $c_{1,0}=1$, and it can be shown that $c_{t,d}\ge 2$ for all other $t$ and $d$. Yet current computationally efficient algorithms show only $c_{t,1}\le 2.25$ and the bound rises quickly to $c_{t,d}\le 3$ for $d\ge 9$. We derive a near-linear-time and essentially sample-optimal estimator that establishes $c_{t,d}=2$ for all $(t,d)\ne(1,0)$. Additionally, for many practical distributions, the lowest approximation distance is achieved by polynomials with vastly varying number of pieces. We provide a method that estimates this number near-optimally, hence helps approach the best possible approximation. Experiments combining the two techniques confirm improved performance over existing methodologies.
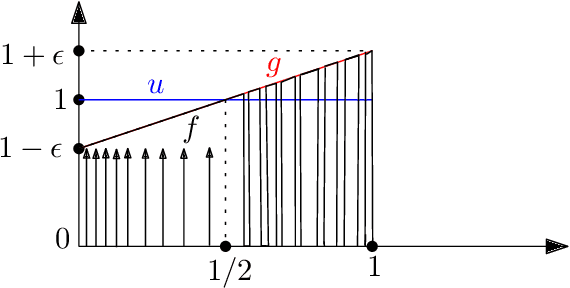
Robust estimation algorithms don't need to know the corruption level
Feb 11, 2022Abstract:Real data are rarely pure. Hence the past half-century has seen great interest in robust estimation algorithms that perform well even when part of the data is corrupt. However, their vast majority approach optimal accuracy only when given a tight upper bound on the fraction of corrupt data. Such bounds are not available in practice, resulting in weak guarantees and often poor performance. This brief note abstracts the complex and pervasive robustness problem into a simple geometric puzzle. It then applies the puzzle's solution to derive a universal meta technique that converts any robust estimation algorithm requiring a tight corruption-level upper bound to achieve its optimal accuracy into one achieving essentially the same accuracy without using any upper bounds.
Linear-Sample Learning of Low-Rank Distributions
Sep 30, 2020
Abstract:Many latent-variable applications, including community detection, collaborative filtering, genomic analysis, and NLP, model data as generated by low-rank matrices. Yet despite considerable research, except for very special cases, the number of samples required to efficiently recover the underlying matrices has not been known. We determine the onset of learning in several common latent-variable settings. For all of them, we show that learning $k\times k$, rank-$r$, matrices to normalized $L_{1}$ distance $\epsilon$ requires $\Omega(\frac{kr}{\epsilon^2})$ samples, and propose an algorithm that uses ${\cal O}(\frac{kr}{\epsilon^2}\log^2\frac r\epsilon)$ samples, a number linear in the high dimension, and nearly linear in the, typically low, rank. The algorithm improves on existing spectral techniques and runs in polynomial time. The proofs establish new results on the rapid convergence of the spectral distance between the model and observation matrices, and may be of independent interest.
Profile Entropy: A Fundamental Measure for the Learnability and Compressibility of Discrete Distributions
Feb 26, 2020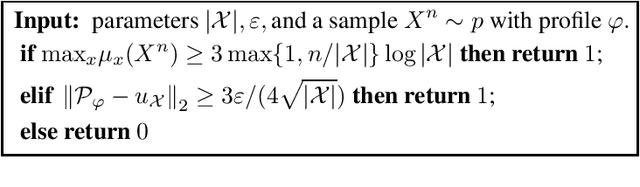
Abstract:The profile of a sample is the multiset of its symbol frequencies. We show that for samples of discrete distributions, profile entropy is a fundamental measure unifying the concepts of estimation, inference, and compression. Specifically, profile entropy a) determines the speed of estimating the distribution relative to the best natural estimator; b) characterizes the rate of inferring all symmetric properties compared with the best estimator over any label-invariant distribution collection; c) serves as the limit of profile compression, for which we derive optimal near-linear-time block and sequential algorithms. To further our understanding of profile entropy, we investigate its attributes, provide algorithms for approximating its value, and determine its magnitude for numerous structural distribution families.
A General Method for Robust Learning from Batches
Feb 25, 2020Abstract:In many applications, data is collected in batches, some of which are corrupt or even adversarial. Recent work derived optimal robust algorithms for estimating discrete distributions in this setting. We consider a general framework of robust learning from batches, and determine the limits of both classification and distribution estimation over arbitrary, including continuous, domains. Building on these results, we derive the first robust agnostic computationally-efficient learning algorithms for piecewise-interval classification, and for piecewise-polynomial, monotone, log-concave, and gaussian-mixture distribution estimation.
SURF: A Simple, Universal, Robust, Fast Distribution Learning Algorithm
Feb 22, 2020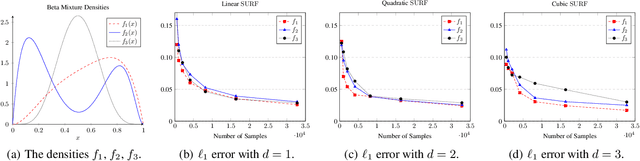
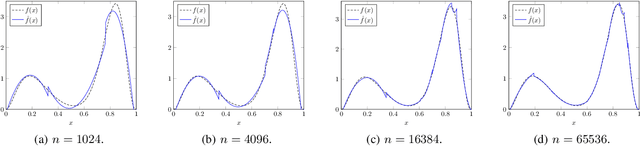
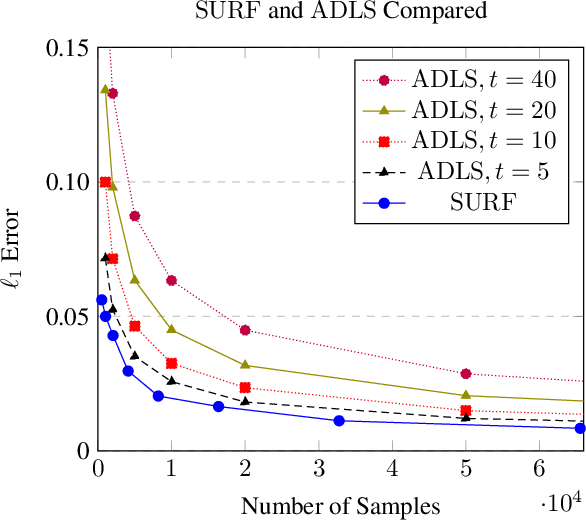

Abstract:Sample- and computationally-efficient distribution estimation is a fundamental tenet in statistics and machine learning. We present $\mathrm{SURF}$, an algorithm for approximating distributions by piecewise polynomials. $\mathrm{SURF}$ is simple, replacing existing general-purpose optimization techniques by straight-forward approximation of each potential polynomial piece by a simple empirical-probability interpolation, and using plain divide-and-conquer to merge the pieces. It is universal, as well-known low-degree polynomial-approximation results imply that it accurately approximates a large class of common distributions. $\mathrm{SURF}$ is robust to distribution mis-specification as for any degree $d\le 8$, it estimates any distribution to an $\ell_1$ distance $ <3 $ times that of the nearest degree-$d$ piecewise polynomial, improving known factor upper bounds of 3 for single polynomials and 15 for polynomials with arbitrarily many pieces. It is fast, using optimal sample complexity, and running in near sample-linear time. In experiments, $\mathrm{SURF}$ significantly outperforms state-of-the art algorithms.
Robust Learning of Discrete Distributions from Batches
Nov 19, 2019
Abstract:Let $d$ be the lowest $L_1$ distance to which a $k$-symbol distribution $p$ can be estimated from $m$ batches of $n$ samples each, when up to $\beta m$ batches may be adversarial. For $\beta<1/2$, Qiao and Valiant (2017) showed that $d=\Omega(\beta/\sqrt{n})$ and requires $m=\Omega(k/\beta^2)$ batches. For $\beta<1/900$, they provided a $d$ and $m$ order-optimal algorithm that runs in time exponential in $k$. For $\beta<0.5$, we propose an algorithm with comparably optimal $d$ and $m$, but run-time polynomial in $k$ and all other parameters.
Unified Sample-Optimal Property Estimation in Near-Linear Time
Nov 08, 2019
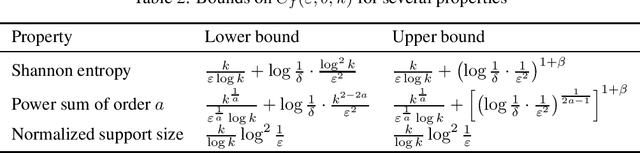
Abstract:We consider the fundamental learning problem of estimating properties of distributions over large domains. Using a novel piecewise-polynomial approximation technique, we derive the first unified methodology for constructing sample- and time-efficient estimators for all sufficiently smooth, symmetric and non-symmetric, additive properties. This technique yields near-linear-time computable estimators whose approximation values are asymptotically optimal and highly-concentrated, resulting in the first: 1) estimators achieving the $\mathcal{O}(k/(\varepsilon^2\log k))$ min-max $\varepsilon$-error sample complexity for all $k$-symbol Lipschitz properties; 2) unified near-optimal differentially private estimators for a variety of properties; 3) unified estimator achieving optimal bias and near-optimal variance for five important properties; 4) near-optimal sample-complexity estimators for several important symmetric properties over both domain sizes and confidence levels. In addition, we establish a McDiarmid's inequality under Poisson sampling, which is of independent interest.
The Broad Optimality of Profile Maximum Likelihood
Jul 11, 2019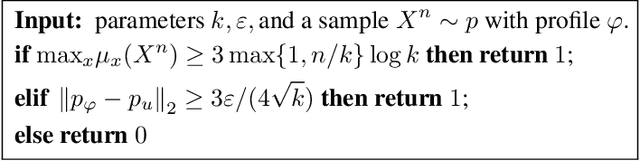
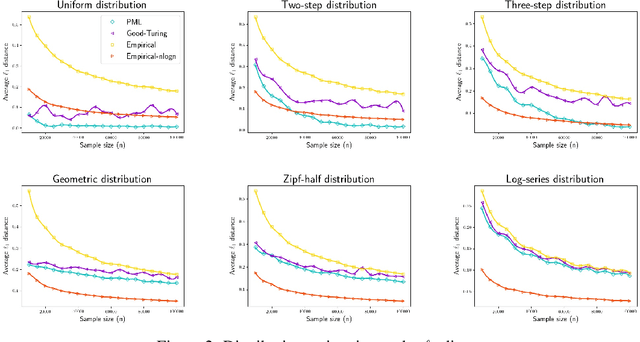
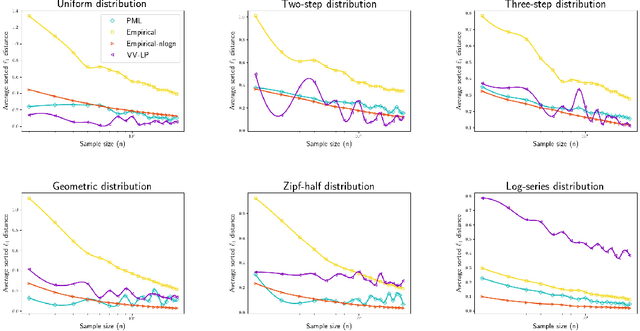
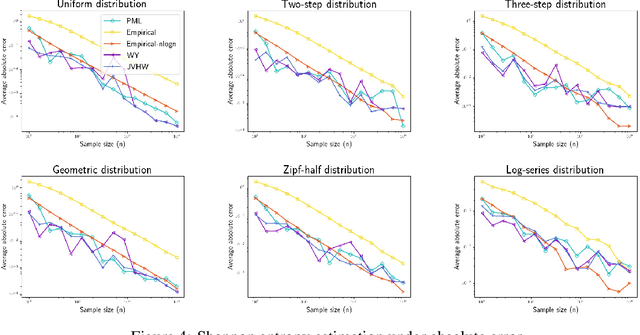
Abstract:We study three fundamental statistical-learning problems: distribution estimation, property estimation, and property testing. We establish the profile maximum likelihood (PML) estimator as the first unified sample-optimal approach to a wide range of learning tasks. In particular, for every alphabet size $k$ and desired accuracy $\varepsilon$: $\textbf{Distribution estimation}$ Under $\ell_1$ distance, PML yields optimal $\Theta(k/(\varepsilon^2\log k))$ sample complexity for sorted-distribution estimation, and a PML-based estimator empirically outperforms the Good-Turing estimator on the actual distribution; $\textbf{Additive property estimation}$ For a broad class of additive properties, the PML plug-in estimator uses just four times the sample size required by the best estimator to achieve roughly twice its error, with exponentially higher confidence; $\boldsymbol{\alpha}\textbf{-R\'enyi entropy estimation}$ For integer $\alpha>1$, the PML plug-in estimator has optimal $k^{1-1/\alpha}$ sample complexity; for non-integer $\alpha>3/4$, the PML plug-in estimator has sample complexity lower than the state of the art; $\textbf{Identity testing}$ In testing whether an unknown distribution is equal to or at least $\varepsilon$ far from a given distribution in $\ell_1$ distance, a PML-based tester achieves the optimal sample complexity up to logarithmic factors of $k$. Most of these results also hold for a near-linear-time computable variant of PML. Stronger results hold for a different and novel variant called truncated PML (TPML).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge