Narae Ryu
Non-backtracking Graph Neural Networks
Oct 11, 2023Abstract:The celebrated message-passing updates for graph neural networks allow the representation of large-scale graphs with local and computationally tractable updates. However, the local updates suffer from backtracking, i.e., a message flows through the same edge twice and revisits the previously visited node. Since the number of message flows increases exponentially with the number of updates, the redundancy in local updates prevents the graph neural network from accurately recognizing a particular message flow for downstream tasks. In this work, we propose to resolve such a redundancy via the non-backtracking graph neural network (NBA-GNN) that updates a message without incorporating the message from the previously visited node. We further investigate how NBA-GNN alleviates the over-squashing of GNNs, and establish a connection between NBA-GNN and the impressive performance of non-backtracking updates for stochastic block model recovery. We empirically verify the effectiveness of our NBA-GNN on long-range graph benchmark and transductive node classification problems.
Regret in Online Recommendation Systems
Oct 23, 2020
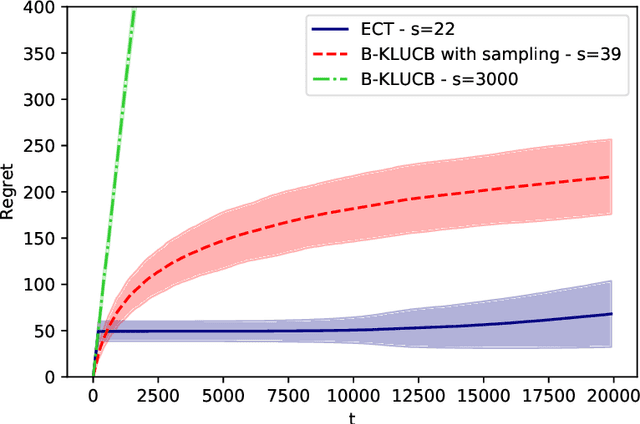


Abstract:This paper proposes a theoretical analysis of recommendation systems in an online setting, where items are sequentially recommended to users over time. In each round, a user, randomly picked from a population of $m$ users, requests a recommendation. The decision-maker observes the user and selects an item from a catalogue of $n$ items. Importantly, an item cannot be recommended twice to the same user. The probabilities that a user likes each item are unknown. The performance of the recommendation algorithm is captured through its regret, considering as a reference an Oracle algorithm aware of these probabilities. We investigate various structural assumptions on these probabilities: we derive for each structure regret lower bounds, and devise algorithms achieving these limits. Interestingly, our analysis reveals the relative weights of the different components of regret: the component due to the constraint of not presenting the same item twice to the same user, that due to learning the chances users like items, and finally that arising when learning the underlying structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge