Regret in Online Recommendation Systems
Paper and Code
Oct 23, 2020
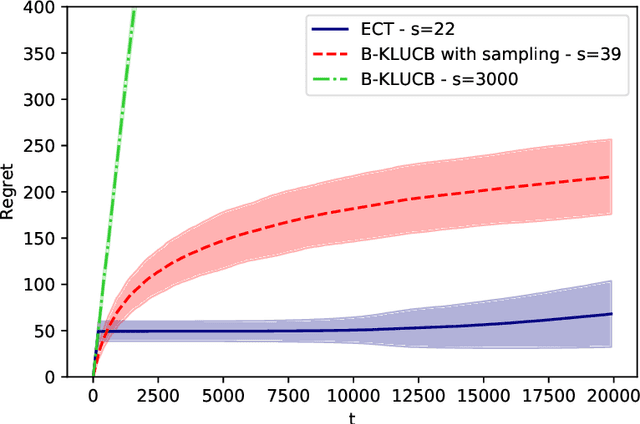


This paper proposes a theoretical analysis of recommendation systems in an online setting, where items are sequentially recommended to users over time. In each round, a user, randomly picked from a population of $m$ users, requests a recommendation. The decision-maker observes the user and selects an item from a catalogue of $n$ items. Importantly, an item cannot be recommended twice to the same user. The probabilities that a user likes each item are unknown. The performance of the recommendation algorithm is captured through its regret, considering as a reference an Oracle algorithm aware of these probabilities. We investigate various structural assumptions on these probabilities: we derive for each structure regret lower bounds, and devise algorithms achieving these limits. Interestingly, our analysis reveals the relative weights of the different components of regret: the component due to the constraint of not presenting the same item twice to the same user, that due to learning the chances users like items, and finally that arising when learning the underlying structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge