Nandan Sriranga
Transmitter Subspace-Aware Target Detection in Two-Channel Passive Radars with Inter-Receiver Collaboration
Sep 16, 2025Abstract:We address target detection in a single Delay-Doppler cell using spatially distributed two-channel passive radars. An unknown illuminator of opportunity (IO) is assumed to emit a waveform lying in a known low-dimensional subspace (e.g., OFDM). Each receiver transforms its reference and surveillance signals onto the IO subspace after noise-whitening, to obtain cross-correlation (CC) measurements. To save bandwidth, receivers collaboratively exchange and linearly combine the CC output, and only a subset transmits them to a fusion center (FC) over a multiple-access channel (MAC). Collaboration weights are designed using the moments of the FC measurement to enhance detection performance.
On Distributed and Asynchronous Sampling of Gaussian Processes for Sequential Binary Hypothesis Testing
Sep 14, 2023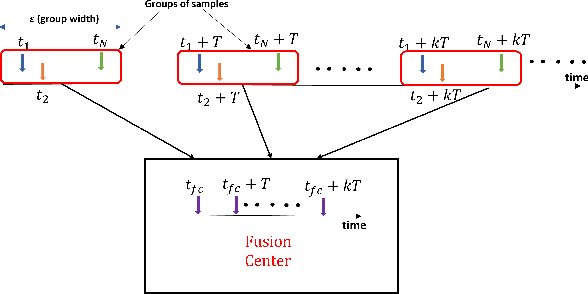
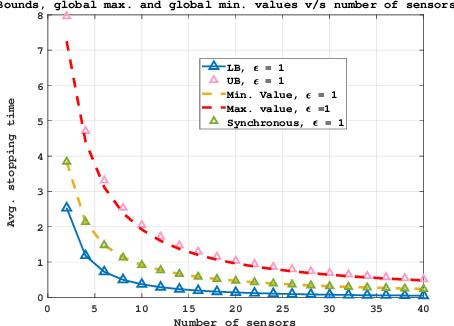
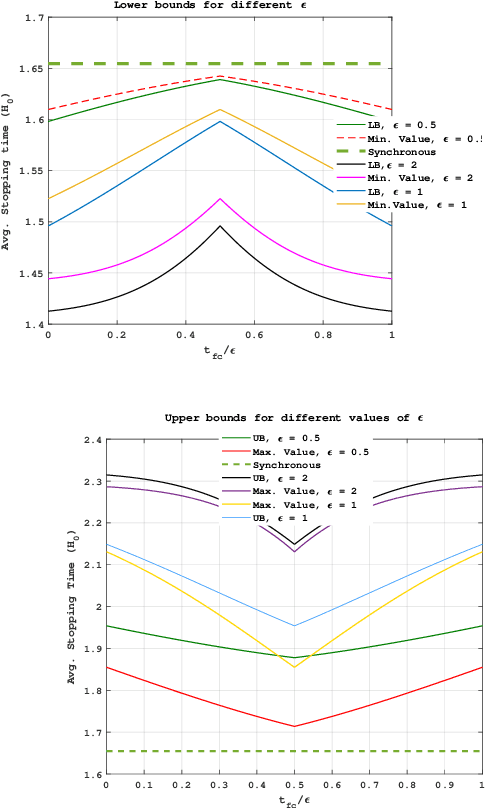
Abstract:In this work, we consider a binary sequential hypothesis testing problem with distributed and asynchronous measurements. The aim is to analyze the effect of sampling times of jointly \textit{wide-sense stationary} (WSS) Gaussian observation processes at distributed sensors on the expected stopping time of the sequential test at the fusion center (FC). The distributed system is such that the sensors and the FC sample observations periodically, where the sampling times are not necessarily synchronous, i.e., the sampling times at different sensors and the FC may be different from each other. \color{black} The sampling times, however, are restricted to be within a time window and a sample obtained within the window is assumed to be \textit{uncorrelated} with samples outside the window. We also assume that correlations may exist only between the observations sampled at the FC and those at the sensors in a pairwise manner (sensor pairs not including the FC have independent observations). The effect of \textit{asynchronous} sampling on the SPRT performance is analyzed by obtaining bounds for the expected stopping time. We illustrate the validity of the theoretical results with numerical results.
Sequential Processing of Observations in Human Decision-Making Systems
Jan 25, 2023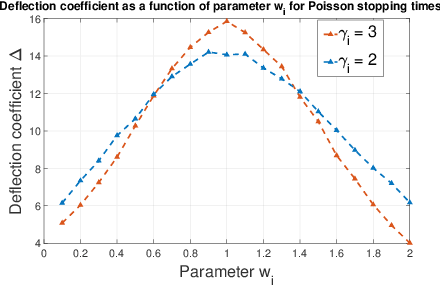
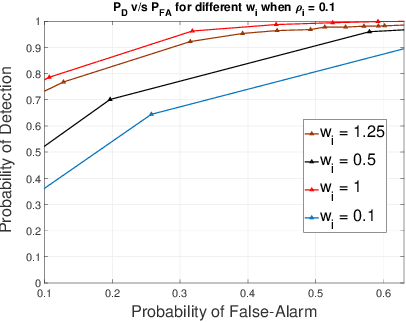
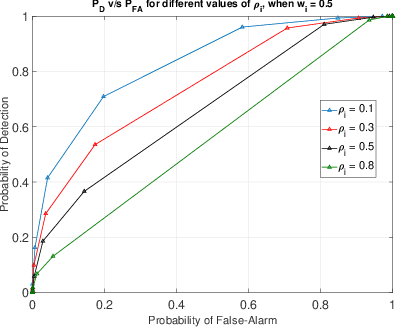
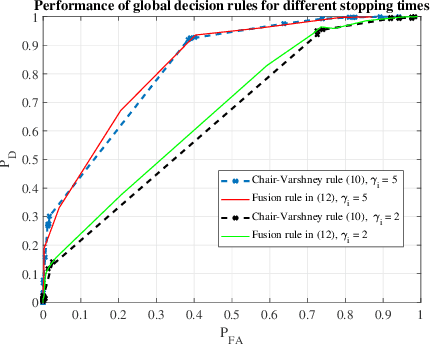
Abstract:In this work, we consider a binary hypothesis testing problem involving a group of human decision-makers. Due to the nature of human behavior, each human decision-maker observes the phenomenon of interest sequentially up to a random length of time. The humans use a belief model to accumulate the log-likelihood ratios until they cease observing the phenomenon. The belief model is used to characterize the perception of the human decision-maker towards observations at different instants of time, i.e., some decision-makers may assign greater importance to observations that were observed earlier, rather than later and vice-versa. The global decision-maker is a machine that fuses human decisions using the Chair-Varshney rule with different weights for the human decisions, where the weights are determined by the number of observations that were used by the humans to arrive at their respective decisions.
Efficient Ordered-Transmission Based Distributed Detection under Data Falsification Attacks
Jul 18, 2022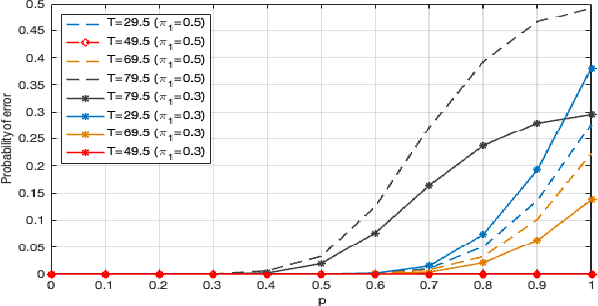
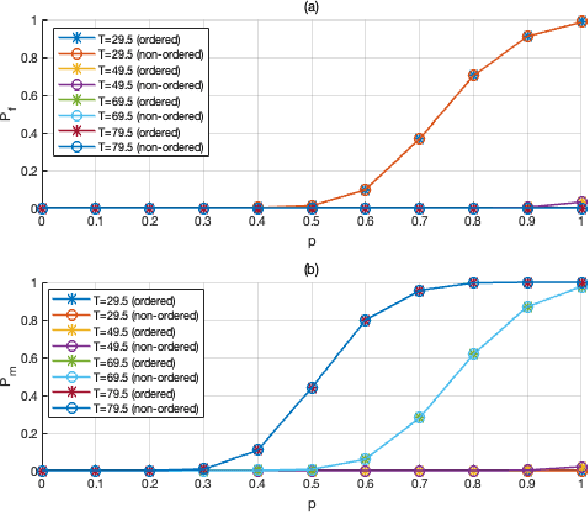
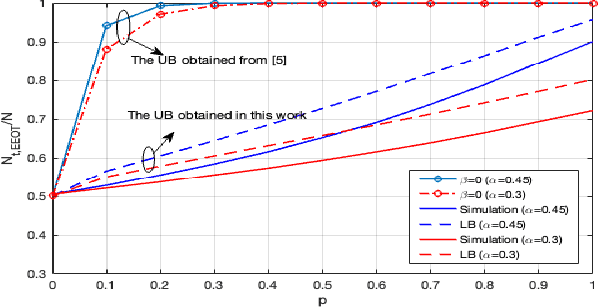
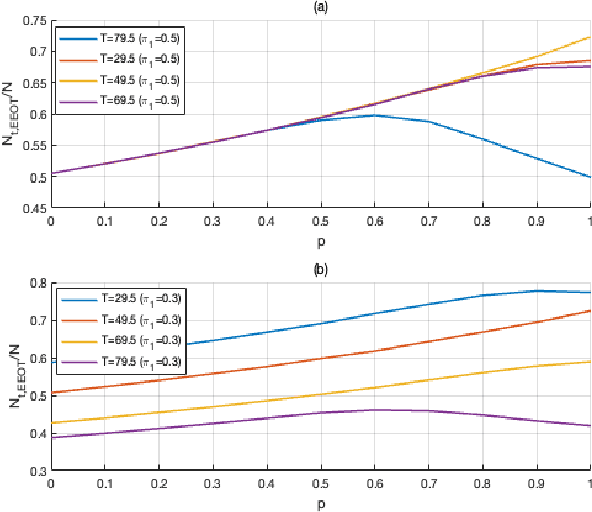
Abstract:In distributed detection systems, energy-efficient ordered transmission (EEOT) schemes are able to reduce the number of transmissions required to make a final decision. In this work, we investigate the effect of data falsification attacks on the performance of EEOT-based systems. We derive the probability of error for an EEOT-based system under attack and find an upper bound (UB) on the expected number of transmissions required to make the final decision. Moreover, we tighten this UB by solving an optimization problem via integer programming (IP). We also obtain the FC's optimal threshold which guarantees the optimal detection performance of the EEOT-based system. Numerical and simulation results indicate that it is possible to reduce transmissions while still ensuring the quality of the decision with an appropriately designed threshold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge