Some Developments in Clustering Analysis on Stochastic Processes

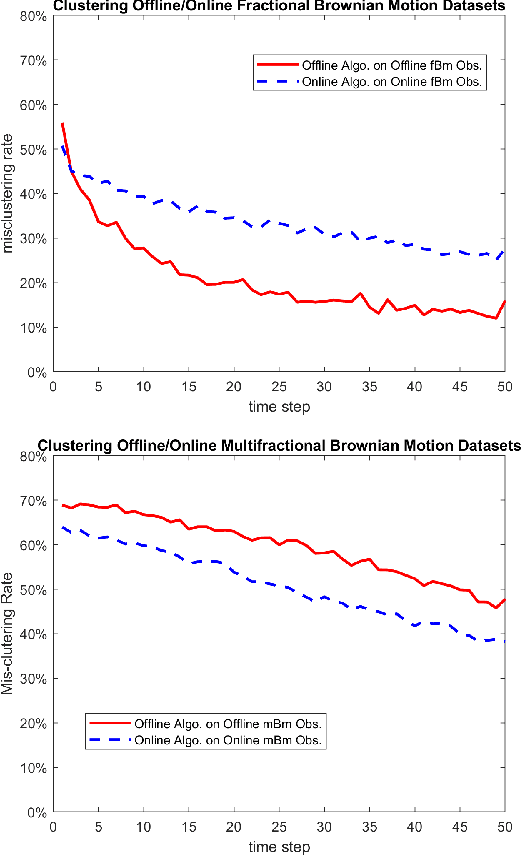
We review some developments on clustering stochastic processes and come with the conclusion that asymptotically consistent clustering algorithms can be obtained when the processes are ergodic and the dissimilarity measure satisfies the triangle inequality. Examples are provided when the processes are distribution ergodic, covariance ergodic and locally asymptotically self-similar, respectively.

Clustering Analysis on Locally Asymptotically Self-similar Processes with Known Number of Clusters

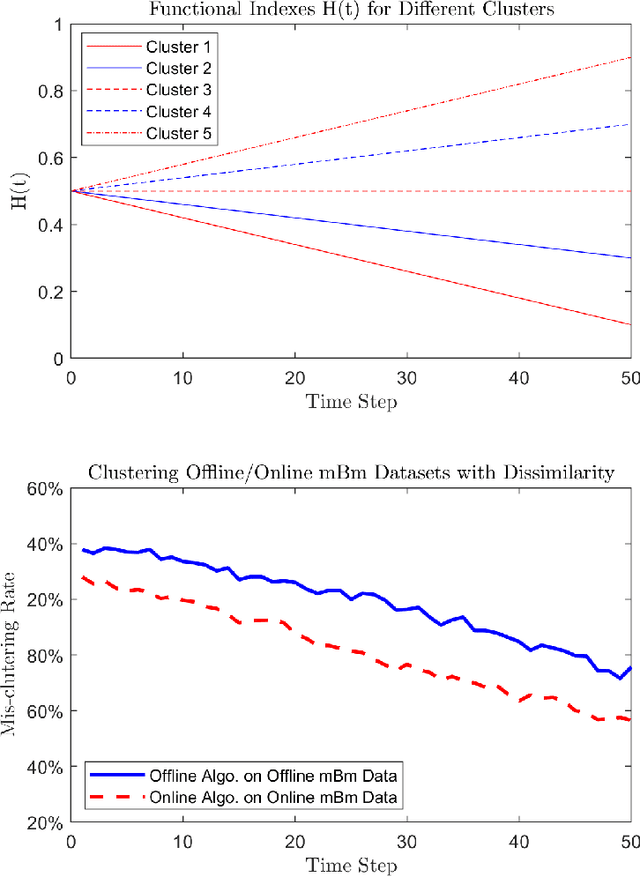
We study the problems of clustering locally asymptotically self-similar stochastic processes, when the true number of clusters is priorly known. A new covariance-based dissimilarity measure is introduced, from which the so-called approximately asymptotically consistent clustering algorithms are obtained. In a simulation study, clustering data sampled from multifractional Brownian motions is performed to illustrate the approximated asymptotic consistency of the proposed algorithms.

Covariance-based Dissimilarity Measures Applied to Clustering Wide-sense Stationary Ergodic Processes

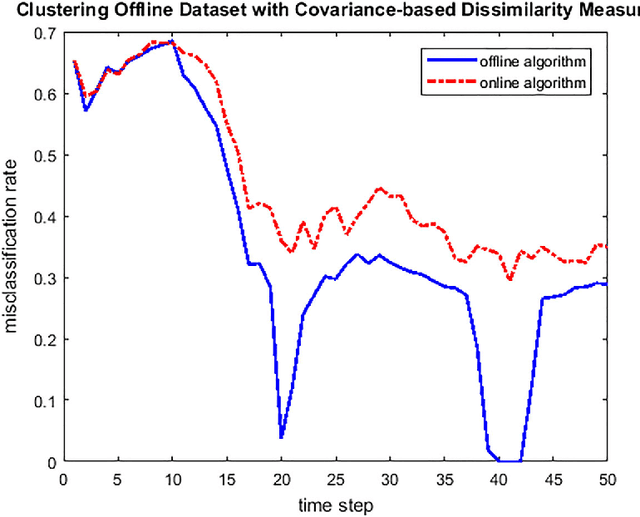
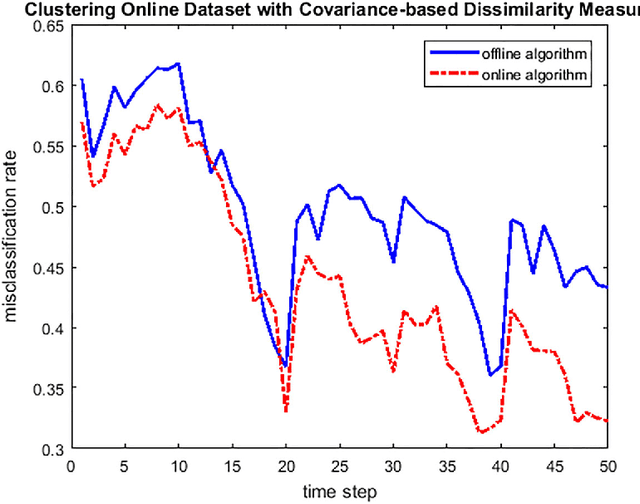
We introduce a new unsupervised learning problem: clustering wide-sense stationary ergodic stochastic processes. A covariance-based dissimilarity measure and consistent algorithms are designed for clustering offline and online data settings, respectively. We also suggest a formal criterion on the efficiency of dissimilarity measures, and discuss of some approach to improve the efficiency of clustering algorithms, when they are applied to cluster particular type of processes, such as self-similar processes with wide-sense stationary ergodic increments. Clustering synthetic data sampled from fractional Brownian motions is provided as an example of application.