Clustering Analysis on Locally Asymptotically Self-similar Processes with Known Number of Clusters
Paper and Code
Nov 04, 2018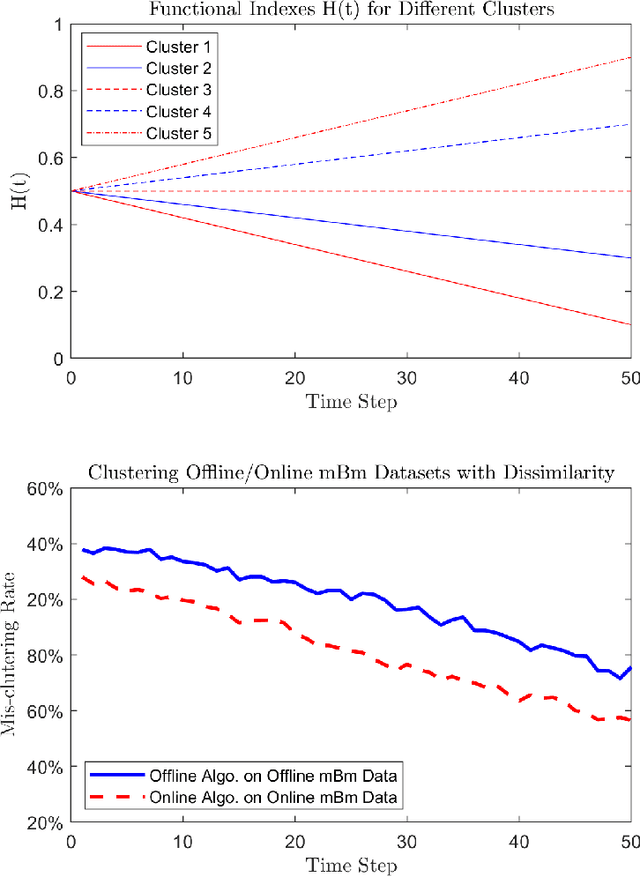
We study the problems of clustering locally asymptotically self-similar stochastic processes, when the true number of clusters is priorly known. A new covariance-based dissimilarity measure is introduced, from which the so-called approximately asymptotically consistent clustering algorithms are obtained. In a simulation study, clustering data sampled from multifractional Brownian motions is performed to illustrate the approximated asymptotic consistency of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge