Robust Trajectory-based Density Estimation for Geometric Structure Recovery: Theory and Applications

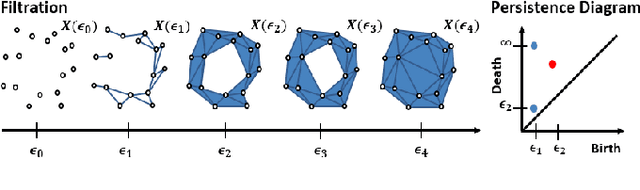
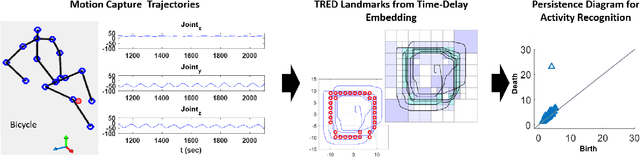
With the rise of the Internet of Things, strategies for effectively processing big data are essential for discovering meaningul insights. The time series datasets produced by groups of interconnected devices contain valuable underlying patterns. Recent works have extracted patterns from spatio-temporal datasets to aid in road network generation, activity recognition, and others. The speed and accuracy of the underlying geometry reconstruction are important in these applications. Existing methods such as kernel density estimation (KDE) have been used but are often computationally expensive. We propose modifying edge quadtrees to utilize their effective heirarchical structure. Our modification estimates density using a novel trajectory count function which provides mathematical guarantees on the stability of the count by enforcing an invariance to local perturbations. We evaluate our method's effectiveness at extracting the underlying geometry and representative subsample points. For verification, we compare against a KDE variant at extracting the underlying shape of noisy synthetic trajectories travelling alonng the shape. We compare map extraction from GPS traces against current methods. Our method significantly improves runtime while extracting the geometry better or at least comparably. We also compare against maxmin subsampling on an activity recognition data set and find a significant runtime improvement with comparable performance.

RULLS: Randomized Union of Locally Linear Subspaces for Feature Engineering

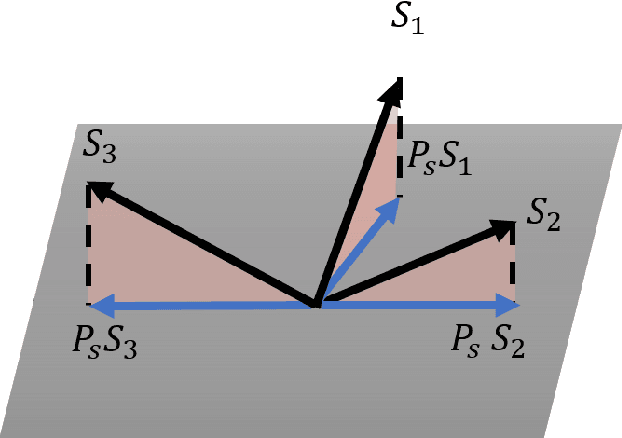
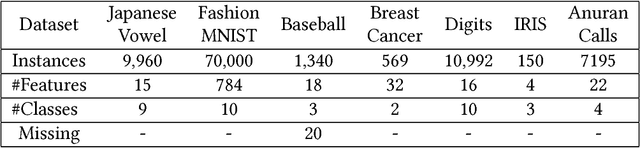
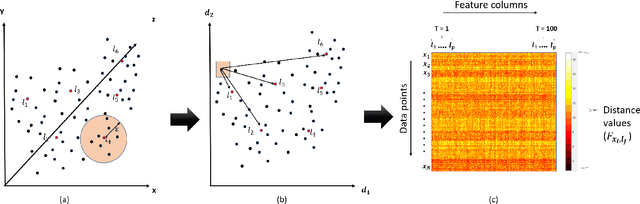
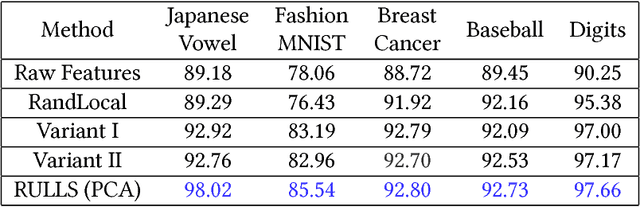
Feature engineering plays an important role in the success of a machine learning model. Most of the effort in training a model goes into data preparation and choosing the right representation. In this paper, we propose a robust feature engineering method, Randomized Union of Locally Linear Subspaces (RULLS). We generate sparse, non-negative, and rotation invariant features in an unsupervised fashion. RULLS aggregates features from a random union of subspaces by describing each point using globally chosen landmarks. These landmarks serve as anchor points for choosing subspaces. Our method provides a way to select features that are relevant in the neighborhood around these chosen landmarks. Distances from each data point to $k$ closest landmarks are encoded in the feature matrix. The final feature representation is a union of features from all chosen subspaces. The effectiveness of our algorithm is shown on various real-world datasets for tasks such as clustering and classification of raw data and in the presence of noise. We compare our method with existing feature generation methods. Results show a high performance of our method on both classification and clustering tasks.