HyperCLOVA X Technical Report

We introduce HyperCLOVA X, a family of large language models (LLMs) tailored to the Korean language and culture, along with competitive capabilities in English, math, and coding. HyperCLOVA X was trained on a balanced mix of Korean, English, and code data, followed by instruction-tuning with high-quality human-annotated datasets while abiding by strict safety guidelines reflecting our commitment to responsible AI. The model is evaluated across various benchmarks, including comprehensive reasoning, knowledge, commonsense, factuality, coding, math, chatting, instruction-following, and harmlessness, in both Korean and English. HyperCLOVA X exhibits strong reasoning capabilities in Korean backed by a deep understanding of the language and cultural nuances. Further analysis of the inherent bilingual nature and its extension to multilingualism highlights the model's cross-lingual proficiency and strong generalization ability to untargeted languages, including machine translation between several language pairs and cross-lingual inference tasks. We believe that HyperCLOVA X can provide helpful guidance for regions or countries in developing their sovereign LLMs.

Aligning Language Models with Preferences through f-divergence Minimization

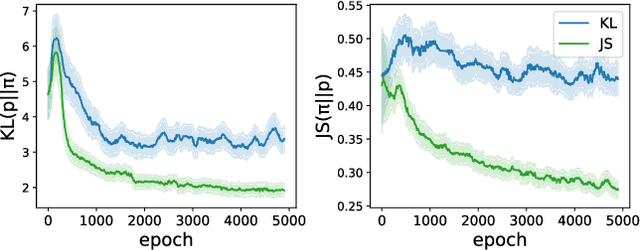
Aligning language models with preferences can be posed as approximating a target distribution representing some desired behavior. Existing approaches differ both in the functional form of the target distribution and the algorithm used to approximate it. For instance, Reinforcement Learning from Human Feedback (RLHF) corresponds to minimizing a reverse KL from an implicit target distribution arising from a KL penalty in the objective. On the other hand, Generative Distributional Control (GDC) has an explicit target distribution and minimizes a forward KL from it using the Distributional Policy Gradient (DPG) algorithm. In this paper, we propose a new approach, f-DPG, which allows the use of any f-divergence to approximate any target distribution. f-DPG unifies both frameworks (RLHF, GDC) and the approximation methods (DPG, RL with KL penalties). We show the practical benefits of various choices of divergence objectives and demonstrate that there is no universally optimal objective but that different divergences are good for approximating different targets. For instance, we discover that for GDC, the Jensen-Shannon divergence frequently outperforms forward KL divergence by a wide margin, leading to significant improvements over prior work.