Achieving Online Regression Performance of LSTMs with Simple RNNs

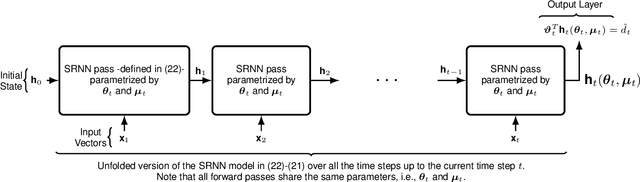
Recurrent Neural Networks (RNNs) are widely used for online regression due to their ability to generalize nonlinear temporal dependencies. As an RNN model, Long-Short-Term-Memory Networks (LSTMs) are commonly preferred in practice, as these networks are capable of learning long-term dependencies while avoiding the vanishing gradient problem. However, due to their large number of parameters, training LSTMs requires considerably longer training time compared to simple RNNs (SRNNs). In this paper, we achieve the online regression performance of LSTMs with SRNNs efficiently. To this end, we introduce a first-order training algorithm with a linear time complexity in the number of parameters. We show that when SRNNs are trained with our algorithm, they provide very similar regression performance with the LSTMs in two to three times shorter training time. We provide strong theoretical analysis to support our experimental results by providing regret bounds on the converge rate of our algorithm. Through an extensive set of experiments, we verify our theoretical work and demonstrate significant performance improvements of our algorithm with respect to LSTMs and the state-of-the-art training methods.

RNN-based Online Learning: An Efficient First-Order Optimization Algorithm with a Convergence Guarantee

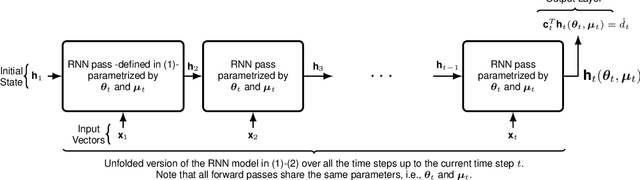
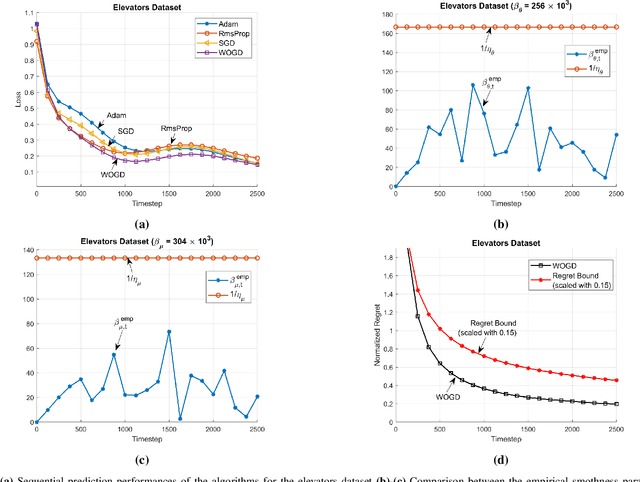
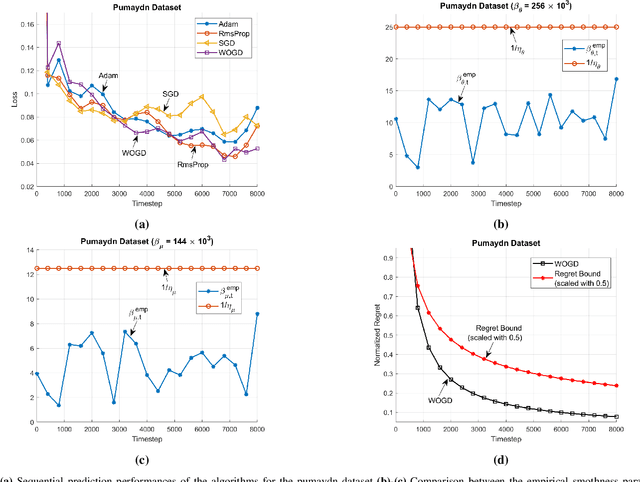
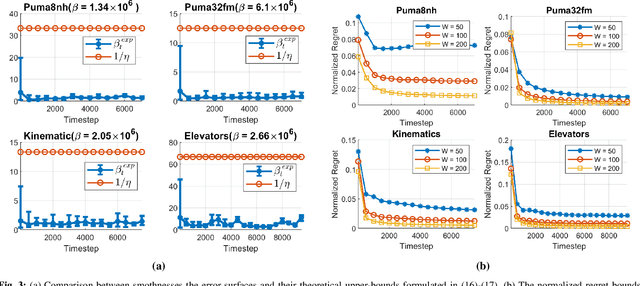
We investigate online nonlinear regression with continually running recurrent neural network networks (RNNs), i.e., RNN-based online learning. For RNN-based online learning, we introduce an efficient first-order training algorithm that theoretically guarantees to converge to the optimum network parameters. Our algorithm is truly online such that it does not make any assumption on the learning environment to guarantee convergence. Through numerical simulations, we verify our theoretical results and illustrate significant performance improvements achieved by our algorithm with respect to the state-of-the-art RNN training methods.

Stability of the Decoupled Extended Kalman Filter Learning Algorithm in LSTM-Based Online Learning

We investigate the convergence and stability properties of the decoupled extended Kalman filter learning algorithm (DEKF) within the long-short term memory network (LSTM) based online learning framework. For this purpose, we model DEKF as a perturbed extended Kalman filter and derive sufficient conditions for its stability during LSTM training. We show that if the perturbations -- introduced due to decoupling -- stay bounded, DEKF learns LSTM parameters with similar convergence and stability properties of the global extended Kalman filter learning algorithm. We verify our results with several numerical simulations and compare DEKF with other LSTM training methods. In our simulations, we also observe that the well-known hyper-parameter selection approaches used for DEKF in the literature satisfy our conditions.

Minimax Optimal Algorithms for Adversarial Bandit Problem with Multiple Plays

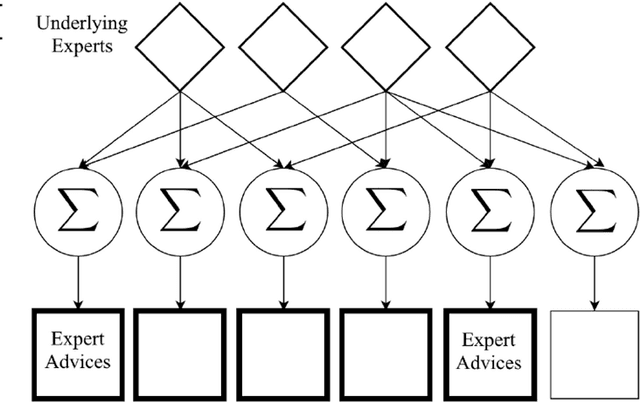
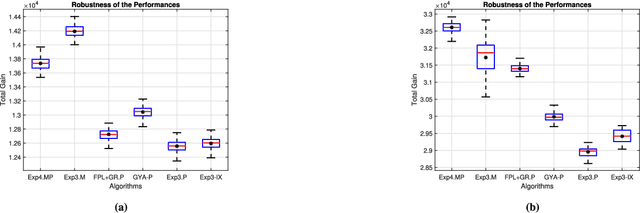
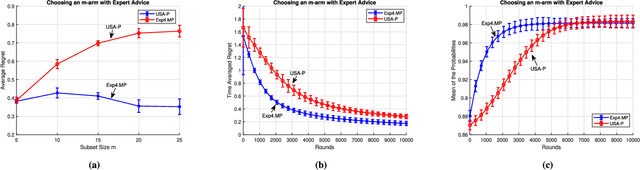
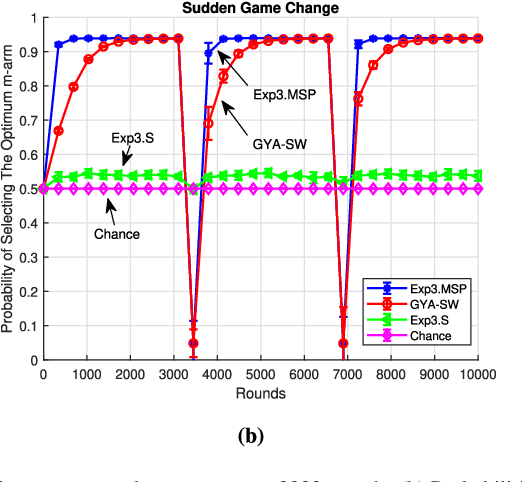
We investigate the adversarial bandit problem with multiple plays under semi-bandit feedback. We introduce a highly efficient algorithm that asymptotically achieves the performance of the best switching $m$-arm strategy with minimax optimal regret bounds. To construct our algorithm, we introduce a new expert advice algorithm for the multiple-play setting. By using our expert advice algorithm, we additionally improve the best-known high-probability bound for the multi-play setting by $O(\sqrt{m})$. Our results are guaranteed to hold in an individual sequence manner since we have no statistical assumption on the bandit arm gains. Through an extensive set of experiments involving synthetic and real data, we demonstrate significant performance gains achieved by the proposed algorithm with respect to the state-of-the-art algorithms.

LSTM-based Online Learning: An Efficient EKF Based Algorithm with a Convergence Guarantee

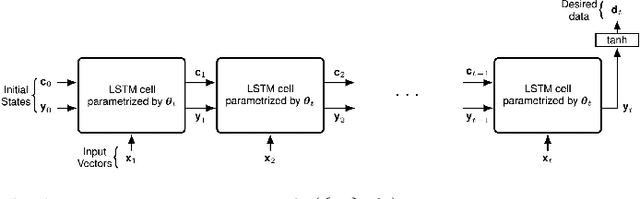
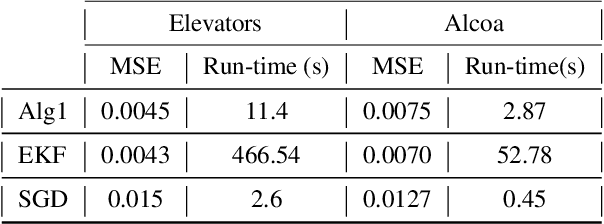
We investigate online nonlinear regression with long short term memory (LSTM) based networks, which we refer to as LSTM-based online learning. For LSTM-based online learning, we introduce a highly efficient extended Kalman filter (EKF) based training algorithm with a theoretical convergence guarantee. Our algorithm is truly online such that it does not make any assumption on the underlying data generating process or the system dynamics of the learning algorithm to guarantee convergence. Through an extensive set of simulations, we illustrate significant performance improvements achieved by our algorithm with respect to the conventional LSTM training methods. We particularly show that our algorithm provides very similar error performance with the EKF learning algorithm in 10-40 times shorter training time depending on the parameter size of the network.