Regret Balancing for Bandit and RL Model Selection

We consider model selection in stochastic bandit and reinforcement learning problems. Given a set of base learning algorithms, an effective model selection strategy adapts to the best learning algorithm in an online fashion. We show that by estimating the regret of each algorithm and playing the algorithms such that all empirical regrets are ensured to be of the same order, the overall regret balancing strategy achieves a regret that is close to the regret of the optimal base algorithm. Our strategy requires an upper bound on the optimal base regret as input, and the performance of the strategy depends on the tightness of the upper bound. We show that having this prior knowledge is necessary in order to achieve a near-optimal regret. Further, we show that any near-optimal model selection strategy implicitly performs a form of regret balancing.

Model Selection in Contextual Stochastic Bandit Problems

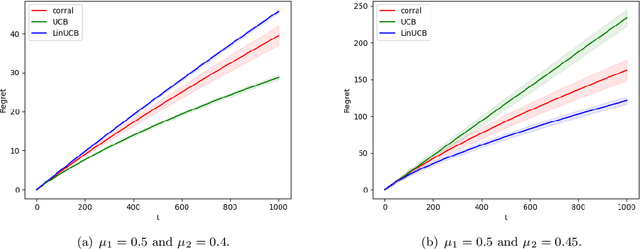
We study model selection in stochastic bandit problems. Our approach relies on a master algorithm that selects its actions among candidate base algorithms. While this problem is studied for specific classes of stochastic base algorithms, our objective is to provide a method that can work with more general classes of stochastic base algorithms. We propose a master algorithm inspired by CORRAL \cite{DBLP:conf/colt/AgarwalLNS17} and introduce a novel and generic smoothing transformation for stochastic bandit algorithms that permits us to obtain $O(\sqrt{T})$ regret guarantees for a wide class of base algorithms when working along with our master. We exhibit a lower bound showing that even when one of the base algorithms has $O(\log T)$ regret, in general it is impossible to get better than $\Omega(\sqrt{T})$ regret in model selection, even asymptotically. We apply our algorithm to choose among different values of $\epsilon$ for the $\epsilon$-greedy algorithm, and to choose between the $k$-armed UCB and linear UCB algorithms. Our empirical studies further confirm the effectiveness of our model-selection method.

Thompson Sampling and Approximate Inference

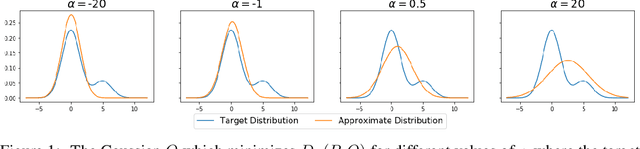
We study the effects of approximate inference on the performance of Thompson sampling in the $k$-armed bandit problems. Thompson sampling is a successful algorithm for online decision-making but requires posterior inference, which often must be approximated in practice. We show that even small constant inference error (in $\alpha$-divergence) can lead to poor performance (linear regret) due to under-exploration (for $\alpha<1$) or over-exploration (for $\alpha>0$) by the approximation. While for $\alpha > 0$ this is unavoidable, for $\alpha \leq 0$ the regret can be improved by adding a small amount of forced exploration even when the inference error is a large constant.