Spectral Statistics of the Sample Covariance Matrix for High Dimensional Linear Gaussians

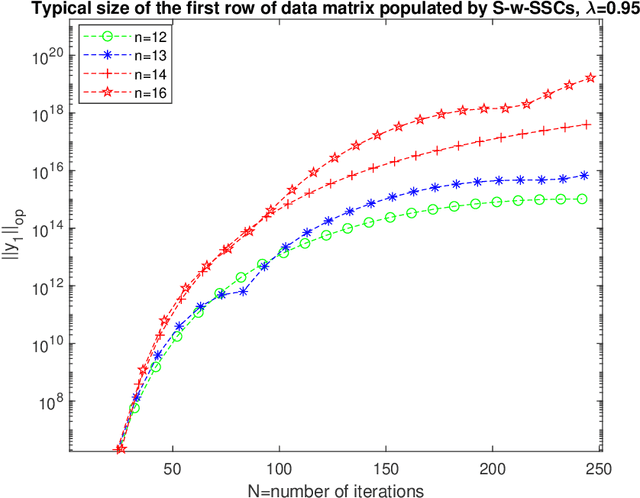
Performance of ordinary least squares(OLS) method for the \emph{estimation of high dimensional stable state transition matrix} $A$(i.e., spectral radius $\rho(A)<1$) from a single noisy observed trajectory of the linear time invariant(LTI)\footnote{Linear Gaussian (LG) in Markov chain literature} system $X_{-}:(x_0,x_1, \ldots,x_{N-1})$ satisfying \begin{equation} x_{t+1}=Ax_{t}+w_{t}, \hspace{10pt} \text{ where } w_{t} \thicksim N(0,I_{n}), \end{equation} heavily rely on negative moments of the sample covariance matrix: $(X_{-}X_{-}^{*})=\sum_{i=0}^{N-1}x_{i}x_{i}^{*}$ and singular values of $EX_{-}^{*}$, where $E$ is a rectangular Gaussian ensemble $E=[w_0, \ldots, w_{N-1}]$. Negative moments requires sharp estimates on all the eigenvalues $\lambda_{1}\big(X_{-}X_{-}^{*}\big) \geq \ldots \geq \lambda_{n}\big(X_{-}X_{-}^{*}\big) \geq 0$. Leveraging upon recent results on spectral theorem for non-Hermitian operators in \cite{naeem2023spectral}, along with concentration of measure phenomenon and perturbation theory(Gershgorins' and Cauchys' interlacing theorem) we show that only when $A=A^{*}$, typical order of $\lambda_{j}\big(X_{-}X_{-}^{*}\big) \in \big[N-n\sqrt{N}, N+n\sqrt{N}\big]$ for all $j \in [n]$. However, in \emph{high dimensions} when $A$ has only one distinct eigenvalue $\lambda$ with geometric multiplicity of one, then as soon as eigenvalue leaves \emph{complex half unit disc}, largest eigenvalue suffers from curse of dimensionality: $\lambda_{1}\big(X_{-}X_{-}^{*}\big)=\Omega\big( \lfloor\frac{N}{n}\rfloor e^{\alpha_{\lambda}n} \big)$, while smallest eigenvalue $\lambda_{n}\big(X_{-}X_{-}^{*}\big) \in (0, N+\sqrt{N}]$. Consequently, OLS estimator incurs a \emph{phase transition} and becomes \emph{transient: increasing iteration only worsens estimation error}, all of this happening when the dynamics are generated from stable systems.

From Spectral Theorem to Statistical Independence with Application to System Identification

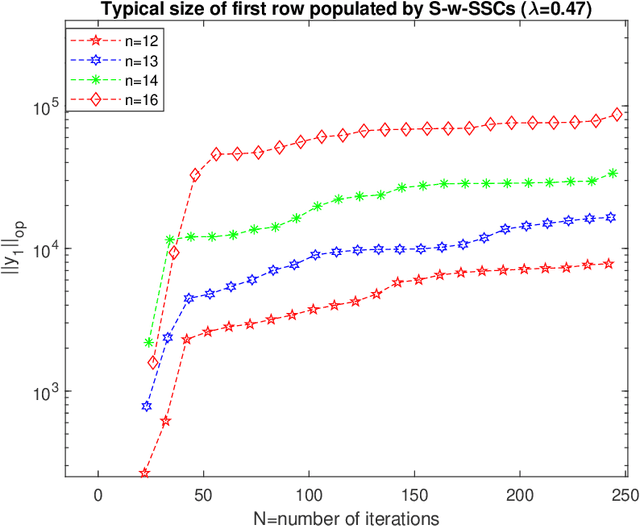
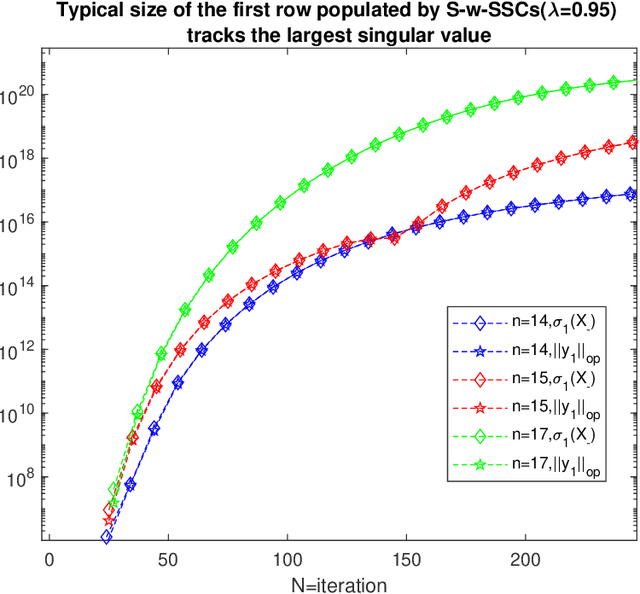
High dimensional random dynamical systems are ubiquitous, including -- but not limited to -- cyber-physical systems, daily return on different stocks of S&P 1500 and velocity profile of interacting particle systems around McKeanVlasov limit. Mathematically, underlying phenomenon can be captured via a stable $n$-dimensional linear transformation `$A$' and additive randomness. System identification aims at extracting useful information about underlying dynamical system, given a length $N$ trajectory from it (corresponds to an $n \times N$ dimensional data matrix). We use spectral theorem for non-Hermitian operators to show that spatio-temperal correlations are dictated by the discrepancy between algebraic and geometric multiplicity of distinct eigenvalues corresponding to state transition matrix. Small discrepancies imply that original trajectory essentially comprises of multiple lower dimensional random dynamical systems living on $A$ invariant subspaces and are statistically independent of each other. In the process, we provide first quantitative handle on decay rate of finite powers of state transition matrix $\|A^{k}\|$ . It is shown that when a stable dynamical system has only one distinct eigenvalue and discrepancy of $n-1$: $\|A\|$ has a dependence on $n$, resulting dynamics are spatially inseparable and consequently there exist at least one row with covariates of typical size $\Theta\big(\sqrt{N-n+1}$ $e^{n}\big)$ i.e., even under stability assumption, covariates can suffer from curse of dimensionality. In the light of these findings we set the stage for non-asymptotic error analysis in estimation of state transition matrix $A$ via least squares regression on observed trajectory by showing that element-wise error is essentially a variant of well-know Littlewood-Offord problem.

Learning and Concentration for High Dimensional Linear Gaussians: an Invariant Subspace Approach

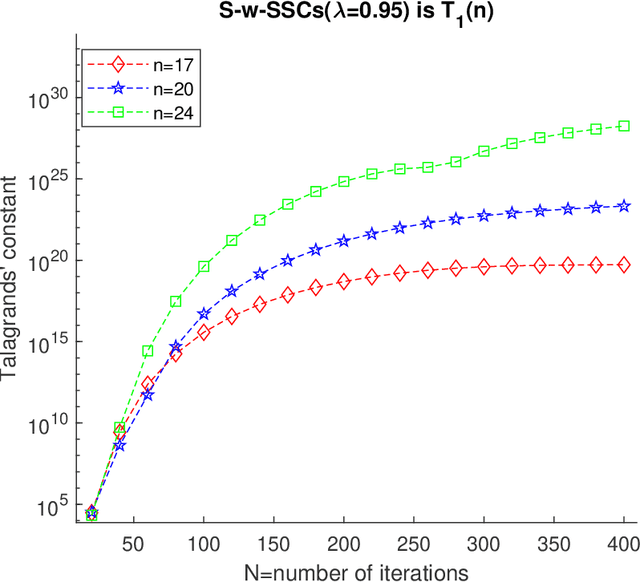
In this work, we study non-asymptotic bounds on correlation between two time realizations of stable linear systems with isotropic Gaussian noise. Consequently, via sampling from a sub-trajectory and using \emph{Talagrands'} inequality, we show that empirical averages of reward concentrate around steady state (dynamical system mixes to when closed loop system is stable under linear feedback policy ) reward , with high-probability. As opposed to common belief of larger the spectral radius stronger the correlation between samples, \emph{large discrepancy between algebraic and geometric multiplicity of system eigenvalues leads to large invariant subspaces related to system-transition matrix}; once the system enters the large invariant subspace it will travel away from origin for a while before coming close to a unit ball centered at origin where an isotropic Gaussian noise can with high probability allow it to escape the current invariant subspace it resides in, leading to \emph{bottlenecks} between different invariant subspaces that span $\mathbb{R}^{n}$, to be precise : system initiated in a large invariant subspace will be stuck there for a long-time: log-linear in dimension of the invariant subspace and inversely to log of inverse of magnitude of the eigenvalue. In the problem of Ordinary Least Squares estimate of system transition matrix via a single trajectory, this phenomenon is even more evident if spectrum of transition matrix associated to large invariant subspace is explosive and small invariant subspaces correspond to stable eigenvalues. Our analysis provide first interpretable and geometric explanation into intricacies of learning and concentration for random dynamical systems on continuous, high dimensional state space; exposing us to surprises in high dimensions

Concentration Phenomenon for Random Dynamical Systems: An Operator Theoretic Approach

Via operator theoretic methods, we formalize the concentration phenomenon for a given observable `$r$' of a discrete time Markov chain with `$\mu_{\pi}$' as invariant ergodic measure, possibly having support on an unbounded state space. The main contribution of this paper is circumventing tedious probabilistic methods with a study of a composition of the Markov transition operator $P$ followed by a multiplication operator defined by $e^{r}$. It turns out that even if the observable/ reward function is unbounded, but for some for some $q>2$, $\|e^{r}\|_{q \rightarrow 2} \propto \exp\big(\mu_{\pi}(r) +\frac{2q}{q-2}\big) $ and $P$ is hyperbounded with norm control $\|P\|_{2 \rightarrow q }< e^{\frac{1}{2}[\frac{1}{2}-\frac{1}{q}]}$, sharp non-asymptotic concentration bounds follow. \emph{Transport-entropy} inequality ensures the aforementioned upper bound on multiplication operator for all $q>2$. The role of \emph{reversibility} in concentration phenomenon is demystified. These results are particularly useful for the reinforcement learning and controls communities as they allow for concentration inequalities w.r.t standard unbounded obersvables/reward functions where exact knowledge of the system is not available, let alone the reversibility of stationary measure.

Transportation-Inequalities, Lyapunov Stability and Sampling for Dynamical Systems on Continuous State Space

We study the concentration phenomenon for discrete-time random dynamical systems with an unbounded state space. We develop a heuristic approach towards obtaining exponential concentration inequalities for dynamical systems using an entirely functional analytic framework. We also show that existence of exponential-type Lyapunov function, compared to the purely deterministic setting, not only implies stability but also exponential concentration inequalities for sampling from the stationary distribution, via \emph{transport-entropy inequality} (T-E). These results have significant impact in \emph{reinforcement learning} (RL) and \emph{controls}, leading to exponential concentration inequalities even for unbounded observables, while neither assuming reversibility nor exact knowledge of random dynamical system (assumptions at heart of concentration inequalities in statistical mechanics and Markov diffusion processes).

Learning Expected Reward for Switched Linear Control Systems: A Non-Asymptotic View

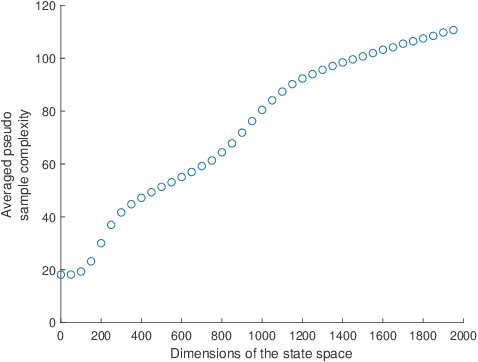
In this work, we show existence of invariant ergodic measure for switched linear dynamical systems (SLDSs) under a norm-stability assumption of system dynamics in some unbounded subset of $\mathbb{R}^{n}$. Consequently, given a stationary Markov control policy, we derive non-asymptotic bounds for learning expected reward (w.r.t the invariant ergodic measure our closed-loop system mixes to) from time-averages using Birkhoff's Ergodic Theorem. The presented results provide a foundation for deriving non-asymptotic analysis for average reward-based optimal control of SLDSs. Finally, we illustrate the presented theoretical results in two case-studies.