Learning Expected Reward for Switched Linear Control Systems: A Non-Asymptotic View
Paper and Code
Jun 15, 2020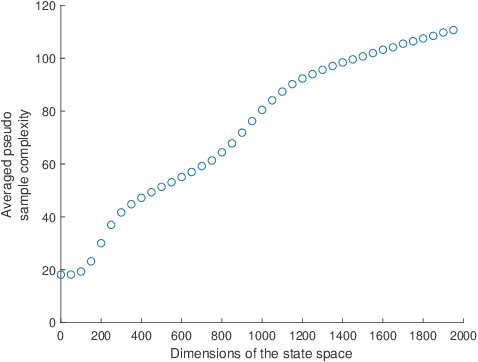
In this work, we show existence of invariant ergodic measure for switched linear dynamical systems (SLDSs) under a norm-stability assumption of system dynamics in some unbounded subset of $\mathbb{R}^{n}$. Consequently, given a stationary Markov control policy, we derive non-asymptotic bounds for learning expected reward (w.r.t the invariant ergodic measure our closed-loop system mixes to) from time-averages using Birkhoff's Ergodic Theorem. The presented results provide a foundation for deriving non-asymptotic analysis for average reward-based optimal control of SLDSs. Finally, we illustrate the presented theoretical results in two case-studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge