Spectral Statistics of the Sample Covariance Matrix for High Dimensional Linear Gaussians
Paper and Code
Dec 10, 2023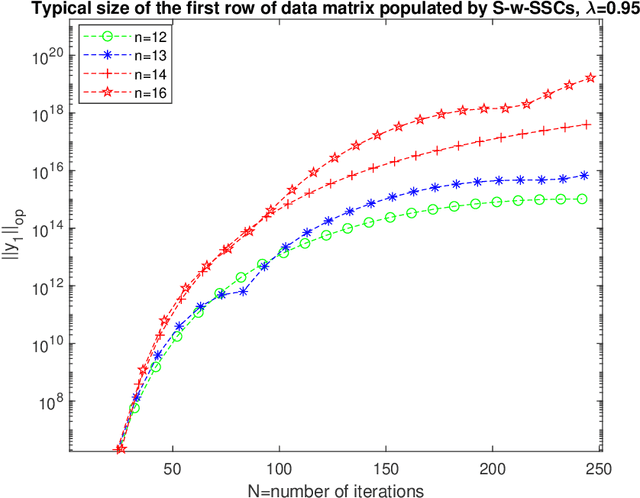
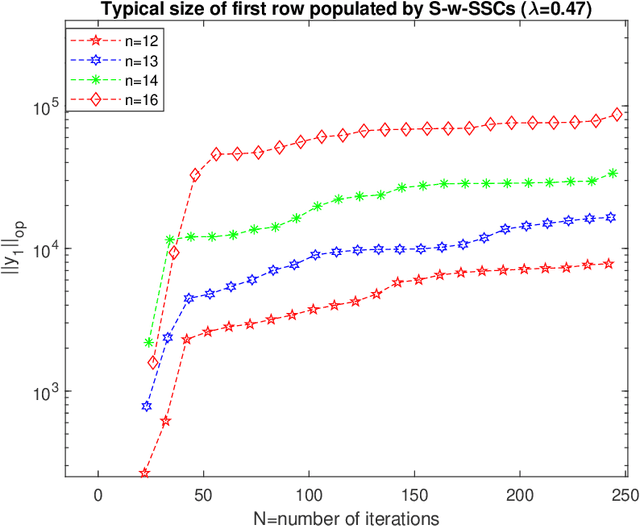
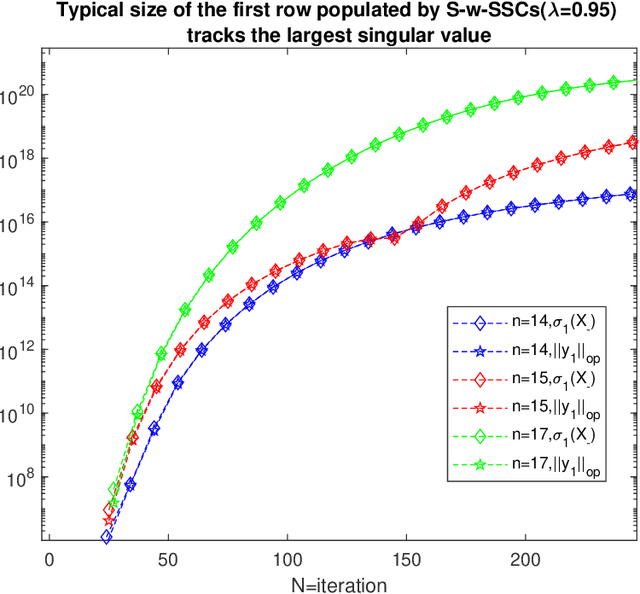
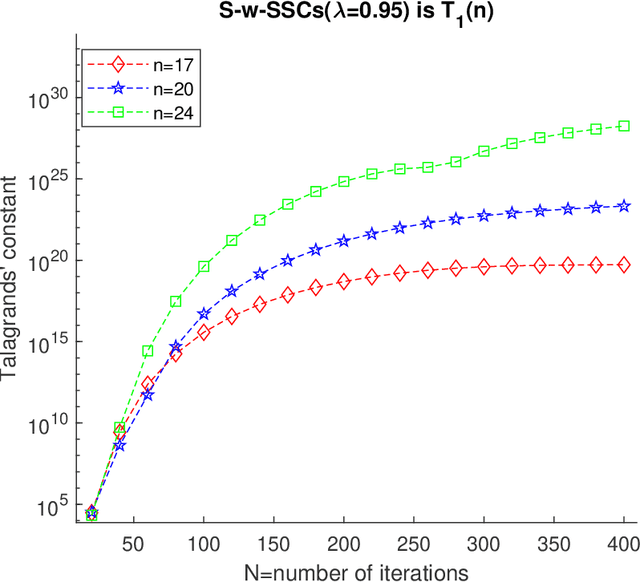
Performance of ordinary least squares(OLS) method for the \emph{estimation of high dimensional stable state transition matrix} $A$(i.e., spectral radius $\rho(A)<1$) from a single noisy observed trajectory of the linear time invariant(LTI)\footnote{Linear Gaussian (LG) in Markov chain literature} system $X_{-}:(x_0,x_1, \ldots,x_{N-1})$ satisfying \begin{equation} x_{t+1}=Ax_{t}+w_{t}, \hspace{10pt} \text{ where } w_{t} \thicksim N(0,I_{n}), \end{equation} heavily rely on negative moments of the sample covariance matrix: $(X_{-}X_{-}^{*})=\sum_{i=0}^{N-1}x_{i}x_{i}^{*}$ and singular values of $EX_{-}^{*}$, where $E$ is a rectangular Gaussian ensemble $E=[w_0, \ldots, w_{N-1}]$. Negative moments requires sharp estimates on all the eigenvalues $\lambda_{1}\big(X_{-}X_{-}^{*}\big) \geq \ldots \geq \lambda_{n}\big(X_{-}X_{-}^{*}\big) \geq 0$. Leveraging upon recent results on spectral theorem for non-Hermitian operators in \cite{naeem2023spectral}, along with concentration of measure phenomenon and perturbation theory(Gershgorins' and Cauchys' interlacing theorem) we show that only when $A=A^{*}$, typical order of $\lambda_{j}\big(X_{-}X_{-}^{*}\big) \in \big[N-n\sqrt{N}, N+n\sqrt{N}\big]$ for all $j \in [n]$. However, in \emph{high dimensions} when $A$ has only one distinct eigenvalue $\lambda$ with geometric multiplicity of one, then as soon as eigenvalue leaves \emph{complex half unit disc}, largest eigenvalue suffers from curse of dimensionality: $\lambda_{1}\big(X_{-}X_{-}^{*}\big)=\Omega\big( \lfloor\frac{N}{n}\rfloor e^{\alpha_{\lambda}n} \big)$, while smallest eigenvalue $\lambda_{n}\big(X_{-}X_{-}^{*}\big) \in (0, N+\sqrt{N}]$. Consequently, OLS estimator incurs a \emph{phase transition} and becomes \emph{transient: increasing iteration only worsens estimation error}, all of this happening when the dynamics are generated from stable systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge