Montserrat Hermo
Automatic White-Box Testing of First-Order Logic Ontologies
Jun 26, 2018
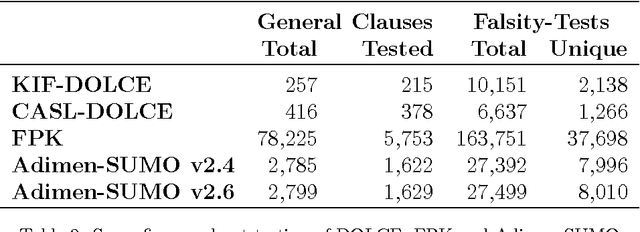

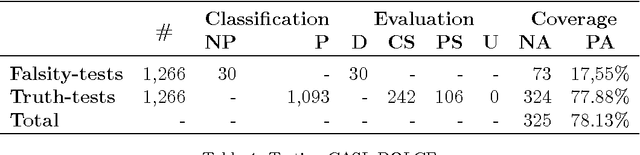
Abstract:Formal ontologies are axiomatizations in a logic-based formalism. The development of formal ontologies, and their important role in the Semantic Web area, is generating considerable research on the use of automated reasoning techniques and tools that help in ontology engineering. One of the main aims is to refine and to improve axiomatizations for enabling automated reasoning tools to efficiently infer reliable information. Defects in the axiomatization can not only cause wrong inferences, but can also hinder the inference of expected information, either by increasing the computational cost of, or even preventing, the inference. In this paper, we introduce a novel, fully automatic white-box testing framework for first-order logic ontologies. Our methodology is based on the detection of inference-based redundancies in the given axiomatization. The application of the proposed testing method is fully automatic since a) the automated generation of tests is guided only by the syntax of axioms and b) the evaluation of tests is performed by automated theorem provers. Our proposal enables the detection of defects and serves to certify the grade of suitability --for reasoning purposes-- of every axiom. We formally define the set of tests that are generated from any axiom and prove that every test is logically related to redundancies in the axiom from which the test has been generated. We have implemented our method and used this implementation to automatically detect several non-trivial defects that were hidden in various first-order logic ontologies. Throughout the paper we provide illustrative examples of these defects, explain how they were found, and how each proof --given by an automated theorem-prover-- provides useful hints on the nature of each defect. Additionally, by correcting all the detected defects, we have obtained an improved version of one of the tested ontologies: Adimen-SUMO.
New Steps on the Exact Learning of CNF
Sep 10, 2016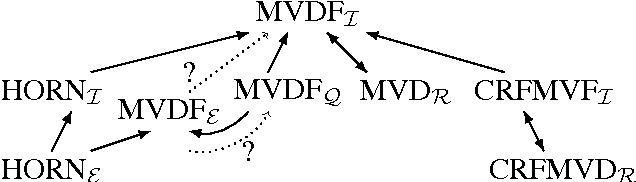
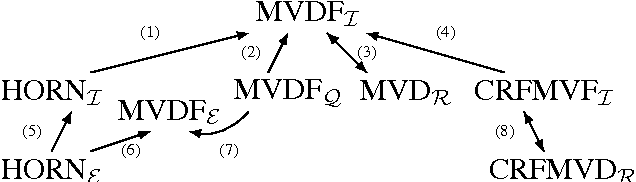
Abstract:A major problem in computational learning theory is whether the class of formulas in conjunctive normal form (CNF) is efficiently learnable. Although it is known that this class cannot be polynomially learned using either membership or equivalence queries alone, it is open whether CNF can be polynomially learned using both types of queries. One of the most important results concerning a restriction of the class CNF is that propositional Horn formulas are polynomial time learnable in Angluin's exact learning model with membership and equivalence queries. In this work we push this boundary and show that the class of multivalued dependency formulas (MVDF) is polynomially learnable from interpretations. We then provide a notion of reduction between learning problems in Angluin's model, showing that a transformation of the algorithm suffices to efficiently learn multivalued database dependencies from data relations. We also show via reductions that our main result extends well known previous results and allows us to find alternative solutions for them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge