GPU accelerated program synthesis: Enumerate semantics, not syntax!

Program synthesis is an umbrella term for generating programs and logical formulae from specifications. With the remarkable performance improvements that GPUs enable for deep learning, a natural question arose: can we also implement a search-based program synthesiser on GPUs to achieve similar performance improvements? In this article we discuss our insights on this question, based on recent works~. The goal is to build a synthesiser running on GPUs which takes as input positive and negative example traces and returns a logical formula accepting the positive and rejecting the negative traces. With GPU-friendly programming techniques -- using the semantics of formulae to minimise data movement and reduce data-dependent branching -- our synthesiser scales to significantly larger synthesis problems, and operates much faster than the previous CPU-based state-of-the-art. We believe the insights that make our approach GPU-friendly have wide potential for enhancing the performance of other formal methods (FM) workloads.

LTL learning on GPUs

Linear temporal logic (LTL) is widely used in industrial verification. LTL formulae can be learned from traces. Scaling LTL formula learning is an open problem. We implement the first GPU-based LTL learner using a novel form of enumerative program synthesis. The learner is sound and complete. Our benchmarks indicate that it handles traces at least 2048 times more numerous, and on average at least 46 times faster than existing state-of-the-art learners. This is achieved with, among others, novel branch-free LTL semantics that has $O(\log n)$ time complexity, where $n$ is trace length, while previous implementations are $O(n^2)$ or worse (assuming bitwise boolean operations and shifts by powers of 2 have unit costs -- a realistic assumption on modern processors).

The Regular Expression Inference Challenge

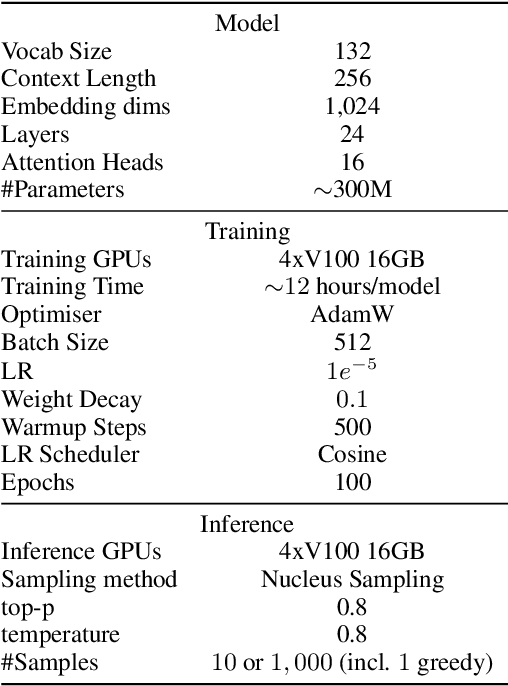
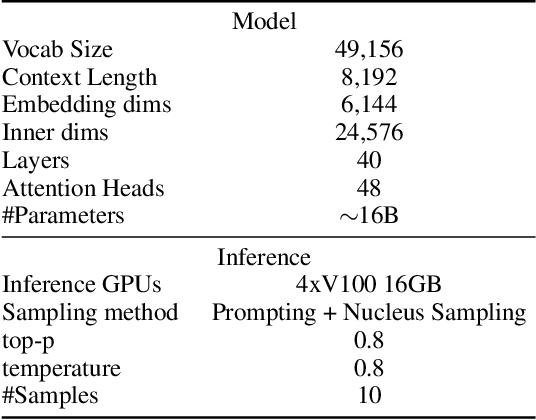
We propose \emph{regular expression inference (REI)} as a challenge for code/language modelling, and the wider machine learning community. REI is a supervised machine learning (ML) and program synthesis task, and poses the problem of finding minimal regular expressions from examples: Given two finite sets of strings $P$ and $N$ and a cost function $\text{cost}(\cdot)$, the task is to generate an expression $r$ that accepts all strings in $P$ and rejects all strings in $N$, while no other such expression $r'$ exists with $\text{cost}(r')<\text{cost}(r)$. REI has advantages as a challenge problem: (i) regular expressions are well-known, widely used, and a natural idealisation of code; (ii) REI's asymptotic worst-case complexity is well understood; (iii) REI has a small number of easy to understand parameters (e.g.~$P$ or $N$ cardinality, string lengths of examples, or the cost function); this lets us easily finetune REI-hardness; (iv) REI is an unsolved problem for deep learning based ML. Recently, an REI solver was implemented on GPUs, using program synthesis techniques. This enabled, for the first time, fast generation of minimal expressions for complex REI instances. Building on this advance, we generate and publish the first large-scale datasets for REI, and devise and evaluate several initial heuristic and machine learning baselines. We invite the community to participate and explore ML methods that learn to solve REI problems. We believe that progress in REI directly translates to code/language modelling.

Search-Based Regular Expression Inference on a GPU

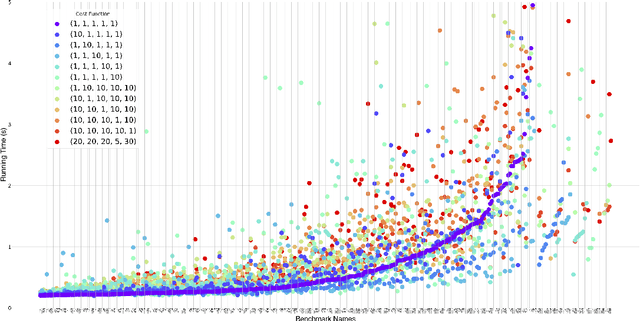
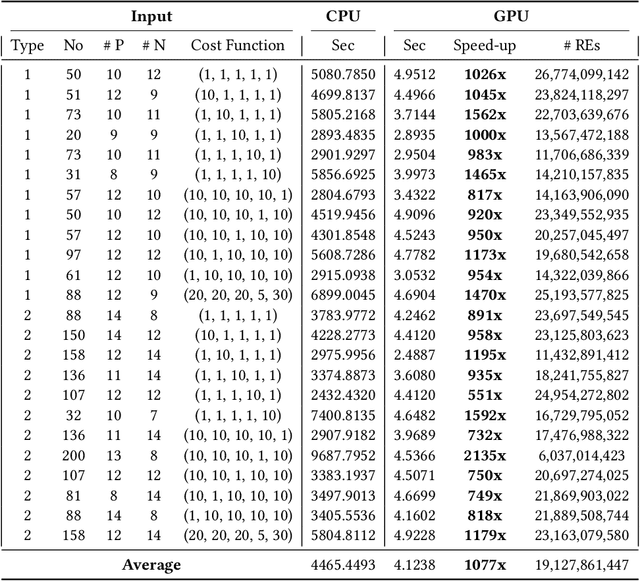
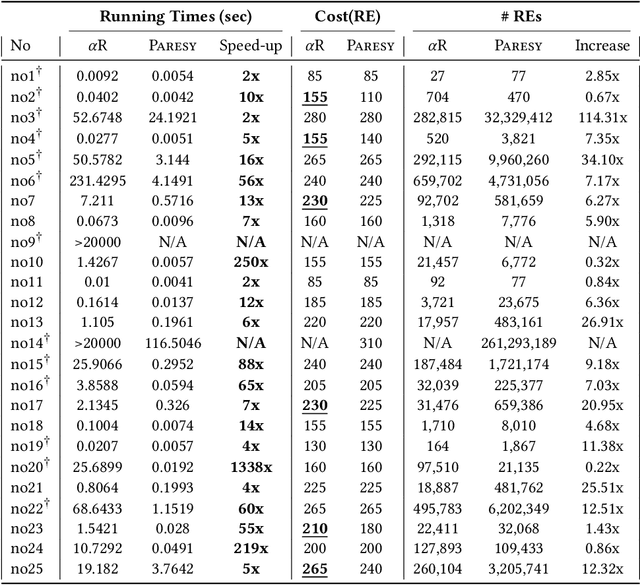
Regular expression inference (REI) is a supervised machine learning and program synthesis problem that takes a cost metric for regular expressions, and positive and negative examples of strings as input. It outputs a regular expression that is precise (i.e., accepts all positive and rejects all negative examples), and minimal w.r.t. to the cost metric. We present a novel algorithm for REI over arbitrary alphabets that is enumerative and trades off time for space. Our main algorithmic idea is to implement the search space of regular expressions succinctly as a contiguous matrix of bitvectors. Collectively, the bitvectors represent, as characteristic sequences, all sub-languages of the infix-closure of the union of positive and negative examples. Mathematically, this is a semiring of (a variant of) formal power series. Infix-closure enables bottom-up compositional construction of larger from smaller regular expressions using the operations of our semiring. This minimises data movement and data-dependent branching, hence maximises data-parallelism. In addition, the infix-closure remains unchanged during the search, hence search can be staged: first pre-compute various expensive operations, and then run the compute intensive search process. We provide two C++ implementations, one for general purpose CPUs and one for Nvidia GPUs (using CUDA). We benchmark both on Google Colab Pro: the GPU implementation is on average over 1000x faster than the CPU implementation on the hardest benchmarks.