Search-Based Regular Expression Inference on a GPU
Paper and Code
May 29, 2023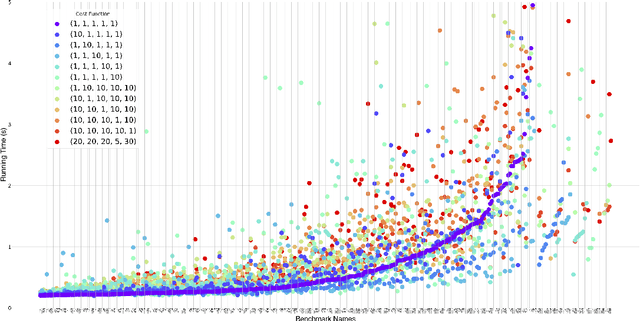
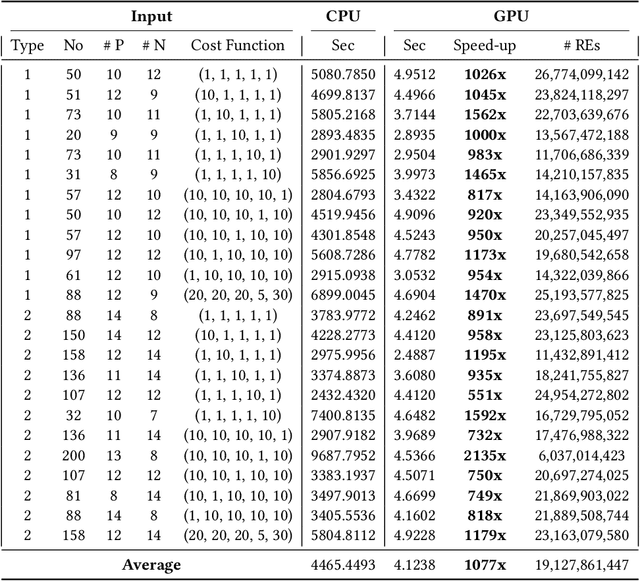
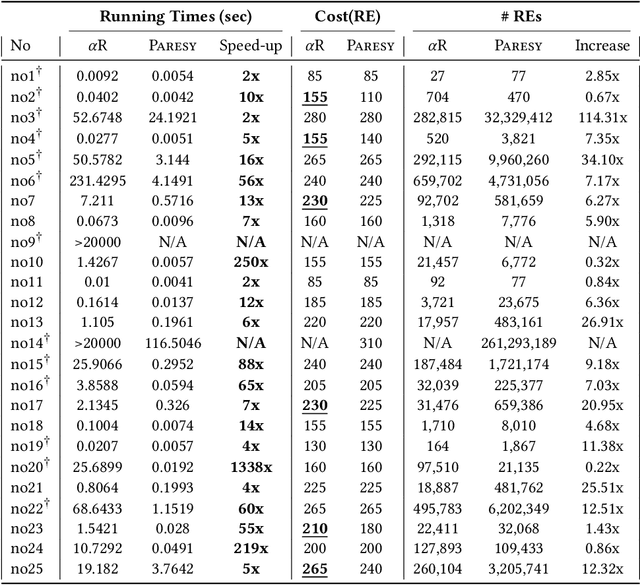
Regular expression inference (REI) is a supervised machine learning and program synthesis problem that takes a cost metric for regular expressions, and positive and negative examples of strings as input. It outputs a regular expression that is precise (i.e., accepts all positive and rejects all negative examples), and minimal w.r.t. to the cost metric. We present a novel algorithm for REI over arbitrary alphabets that is enumerative and trades off time for space. Our main algorithmic idea is to implement the search space of regular expressions succinctly as a contiguous matrix of bitvectors. Collectively, the bitvectors represent, as characteristic sequences, all sub-languages of the infix-closure of the union of positive and negative examples. Mathematically, this is a semiring of (a variant of) formal power series. Infix-closure enables bottom-up compositional construction of larger from smaller regular expressions using the operations of our semiring. This minimises data movement and data-dependent branching, hence maximises data-parallelism. In addition, the infix-closure remains unchanged during the search, hence search can be staged: first pre-compute various expensive operations, and then run the compute intensive search process. We provide two C++ implementations, one for general purpose CPUs and one for Nvidia GPUs (using CUDA). We benchmark both on Google Colab Pro: the GPU implementation is on average over 1000x faster than the CPU implementation on the hardest benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge