Robust Heterogeneous Analog-Digital Computing for Mixture-of-Experts Models with Theoretical Generalization Guarantees

Sparse Mixture-of-Experts (MoE) models enable efficient scalability by activating only a small sub-set of experts per input, yet their massive parameter counts lead to substantial memory and energy inefficiency during inference. Analog in-memory computing (AIMC) offers a promising solution by eliminating frequent data movement between memory and compute units. However, mitigating hardware nonidealities of AIMC typically requires noise-aware retraining, which is infeasible for large MoE models. In this paper, we propose a retraining-free heterogeneous computation framework in which noise-sensitive experts, which are provably identifiable by their maximum neuron norm, are computed digitally while the majority of the experts are executed on AIMC hardware. We further assign densely activated modules, such as attention layers, to digital computation due to their high noise sensitivity despite comprising a small fraction of parameters. Extensive experiments on large MoE language models, including DeepSeekMoE and OLMoE, across multiple benchmark tasks validate the robustness of our approach in maintaining accuracy under analog nonidealities.

A Provably Effective Method for Pruning Experts in Fine-tuned Sparse Mixture-of-Experts

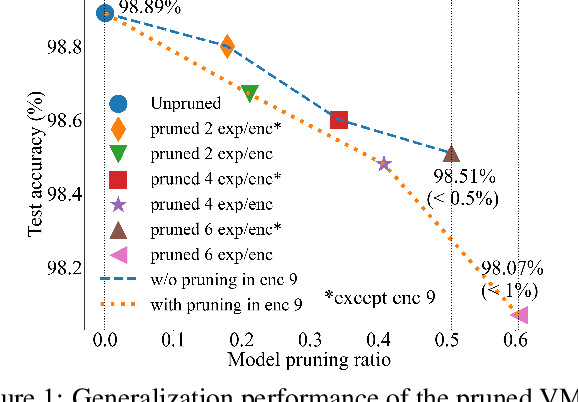
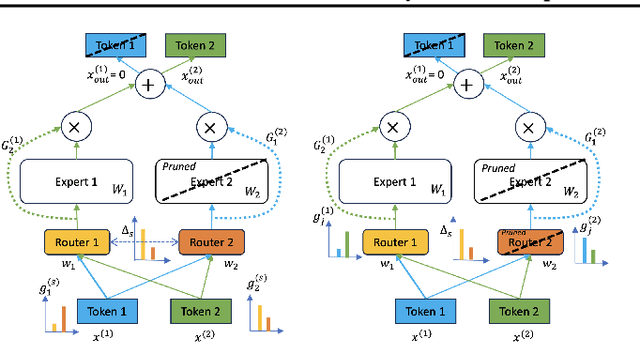
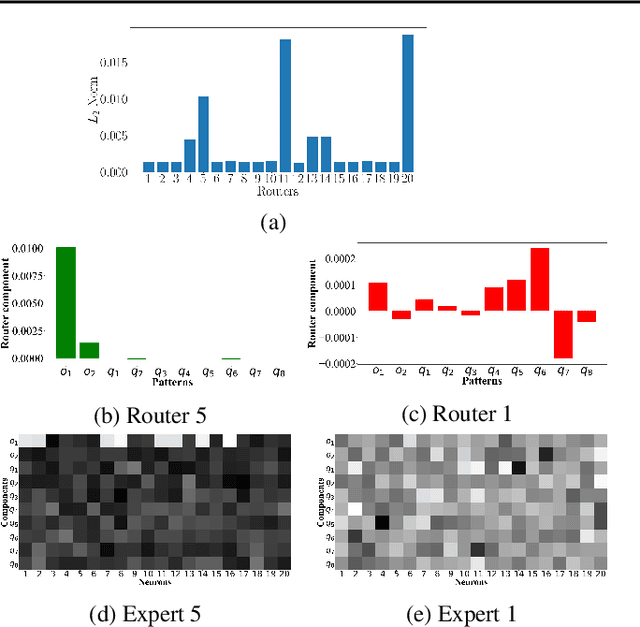
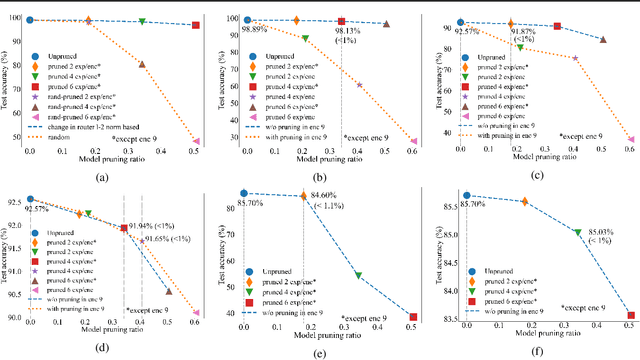
The sparsely gated mixture of experts (MoE) architecture sends different inputs to different subnetworks, i.e., experts, through trainable routers. MoE reduces the training computation significantly for large models, but its deployment can be still memory or computation expensive for some downstream tasks. Model pruning is a popular approach to reduce inference computation, but its application in MoE architecture is largely unexplored. To the best of our knowledge, this paper provides the first provably efficient technique for pruning experts in finetuned MoE models. We theoretically prove that prioritizing the pruning of the experts with a smaller change of the routers l2 norm from the pretrained model guarantees the preservation of test accuracy, while significantly reducing the model size and the computational requirements. Although our theoretical analysis is centered on binary classification tasks on simplified MoE architecture, our expert pruning method is verified on large vision MoE models such as VMoE and E3MoE finetuned on benchmark datasets such as CIFAR10, CIFAR100, and ImageNet.

Patch-level Routing in Mixture-of-Experts is Provably Sample-efficient for Convolutional Neural Networks

In deep learning, mixture-of-experts (MoE) activates one or few experts (sub-networks) on a per-sample or per-token basis, resulting in significant computation reduction. The recently proposed \underline{p}atch-level routing in \underline{MoE} (pMoE) divides each input into $n$ patches (or tokens) and sends $l$ patches ($l\ll n$) to each expert through prioritized routing. pMoE has demonstrated great empirical success in reducing training and inference costs while maintaining test accuracy. However, the theoretical explanation of pMoE and the general MoE remains elusive. Focusing on a supervised classification task using a mixture of two-layer convolutional neural networks (CNNs), we show for the first time that pMoE provably reduces the required number of training samples to achieve desirable generalization (referred to as the sample complexity) by a factor in the polynomial order of $n/l$, and outperforms its single-expert counterpart of the same or even larger capacity. The advantage results from the discriminative routing property, which is justified in both theory and practice that pMoE routers can filter label-irrelevant patches and route similar class-discriminative patches to the same expert. Our experimental results on MNIST, CIFAR-10, and CelebA support our theoretical findings on pMoE's generalization and show that pMoE can avoid learning spurious correlations.