Kalman Filtering for Precise Indoor Position and Orientation Estimation Using IMU and Acoustics on Riemannian Manifolds

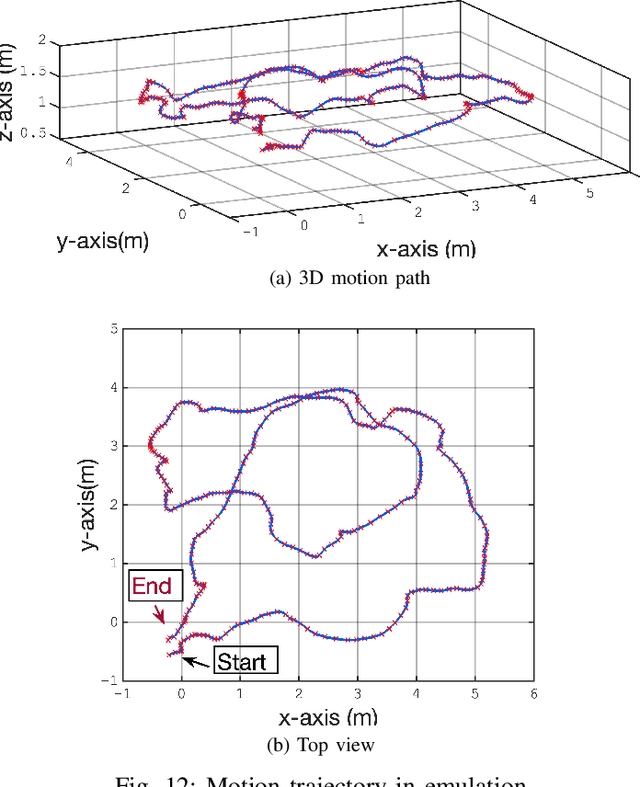
Indoor tracking and pose estimation, i.e., determining the position and orientation of a moving target, are increasingly important due to their numerous applications. While Inertial Navigation Systems (INS) provide high update rates, their positioning errors can accumulate rapidly over time. To mitigate this, it is common to integrate INS with complementary systems to correct drift and improve accuracy. This paper presents a novel approach that combines INS with an acoustic Riemannian-based localization system to enhance indoor positioning and orientation tracking. The proposed method employs both the Extended Kalman Filter (EKF) and the Unscented Kalman Filter (UKF) for fusing data from the two systems. The Riemannian-based localization system delivers high-accuracy estimates of the target's position and orientation, which are then used to correct the INS data. A new projection algorithm is introduced to map the EKF or UKF output onto the Riemannian manifold, further improving estimation accuracy. Our results show that the proposed methods significantly outperform benchmark algorithms in both position and orientation estimation. The effectiveness of the proposed methods was evaluated through extensive numerical simulations and testing using our in-house experimental setup. These evaluations confirm the superior performance of our approach in practical scenarios.

Manifold Optimization for High Accuracy Spatial Location Estimation Using Ultrasound Waves

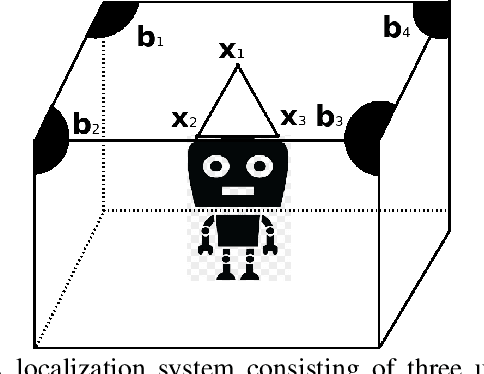
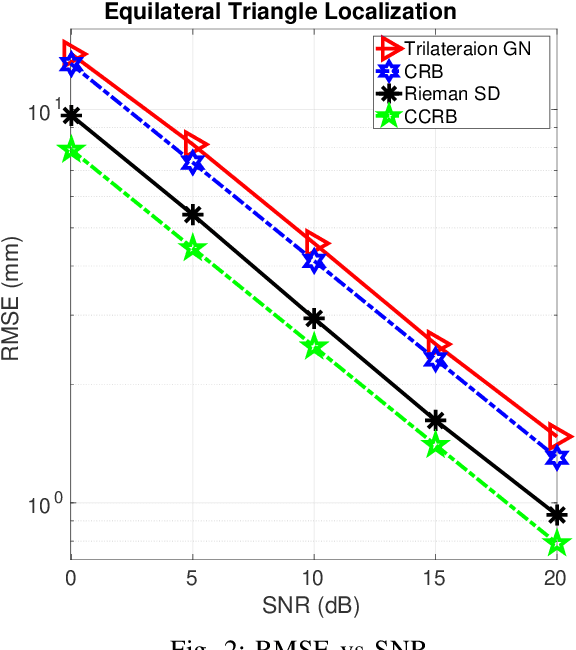
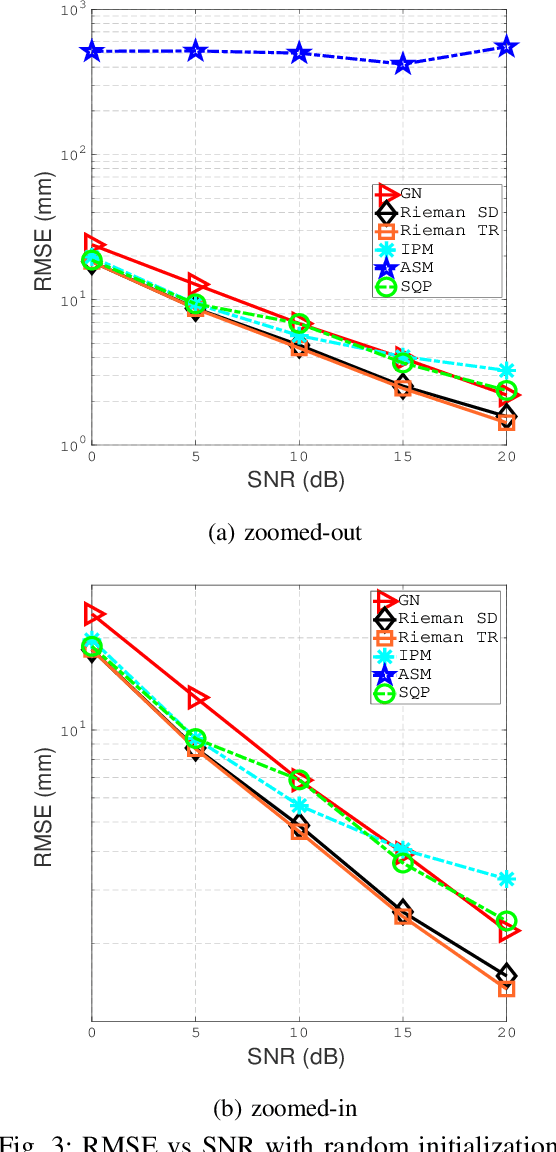
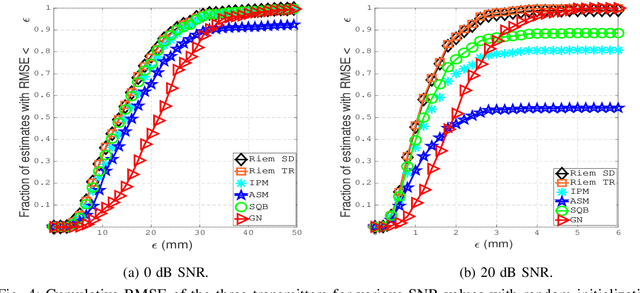
This paper designs a high accuracy spatial location estimation method using ultrasound waves by exploiting the fixed geometry of the transmitters. Assuming an equilateral triangle antenna configuration, where three antennas are placed as the vertices of an equilateral triangle, the spatial location problem can be formulated as a non-convex optimization problem whose interior is shown to admit a Riemannian manifold structure. The investigation of the geometry of the newly introduced manifold, i.e. the manifold of all equilateral triangles in R^3, allows the design of highly efficient optimization algorithms. Simulation results are presented to compare the performance of the proposed approach against popular methods from the literature. The results suggest that the proposed Riemannian-based methods outperform the state-of-the-art methods. Furthermore, the proposed Riemannian methods require much smaller computation time as compared with popular generic non-convex approaches.

Range Estimation of a Moving Target Using Ultrasound Differential Zadoff-Chu Codes

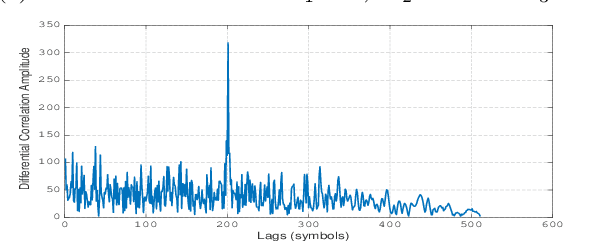
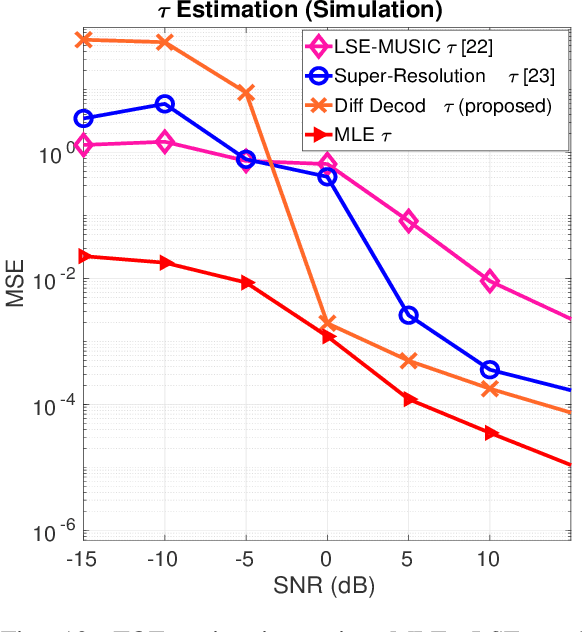
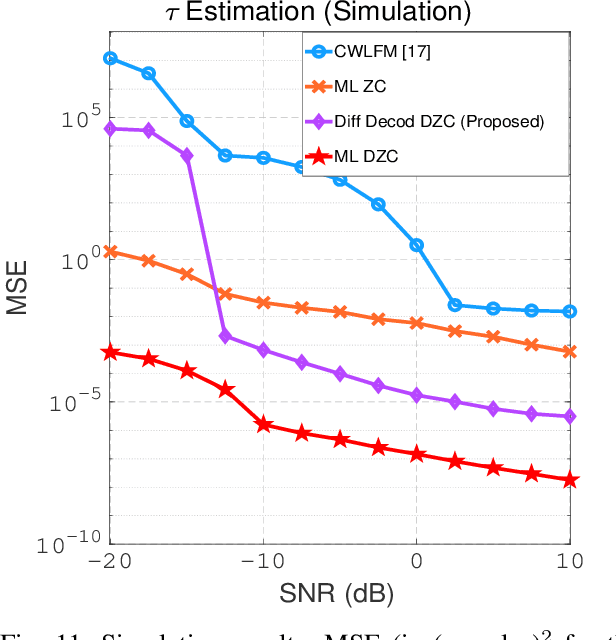
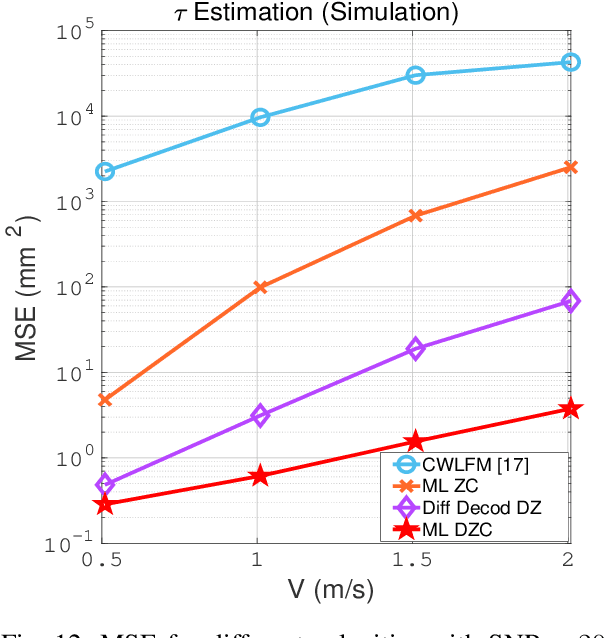
High accuracy range estimation is an essential tool required in many modern applications and technologies. However, continuous range estimation of a moving target is a challenging task, especially under Doppler effects. This paper presents a novel signal design, which we name differential Zadoff-Chu (DZC). Under Doppler effects, DZC sequences improve the performance of the maximum likelihood (ML)-based range estimation compared to its performance when using regular ZC sequences. Moreover, a reduced-complexity ranging algorithm is proposed utilizing DZC sequences and is shown to outperform the regular ZC ML-based range estimation. The proposed system is evaluated in a typical indoor environment, using low-cost ultrasound hardware. Under a low signal to noise ratio (-10 dB SNR), more than 90% of the range estimates are in less than 1.6 mm error, with a movement range from $0.2$ m to 2.2 m and a maximum velocity of 0.5 m/s. For the same movement range, the system provides range estimates with a root mean square error (RMSE) less than 0.76 mm in a high SNR scenario (10 dB), and an MSE less than 0.85 mm in a low SNR scenario (-10 dB). For a larger movement range from 1.8 m to 4.2 m with a maximum velocity of 1.91 m/s, the proposed system provides range estimates with RMSE less than 7.70 mm at 10 dB SNR.