Fine Grained Analysis and Optimization of Large Scale Automotive Radar Networks

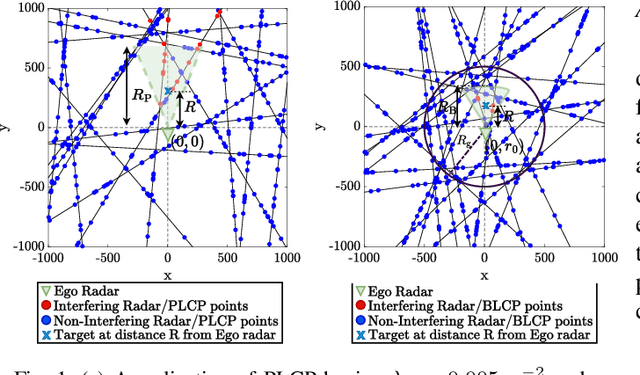
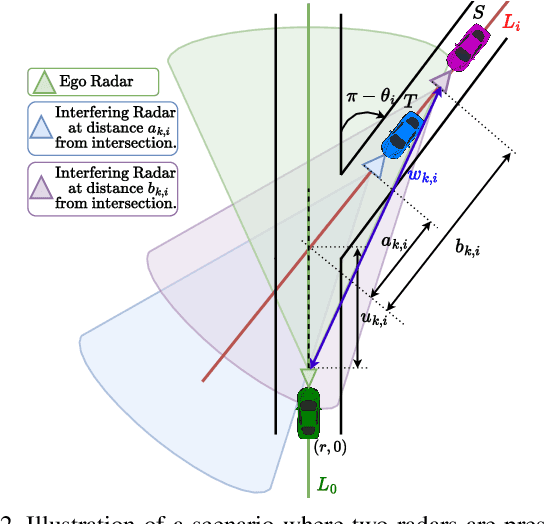
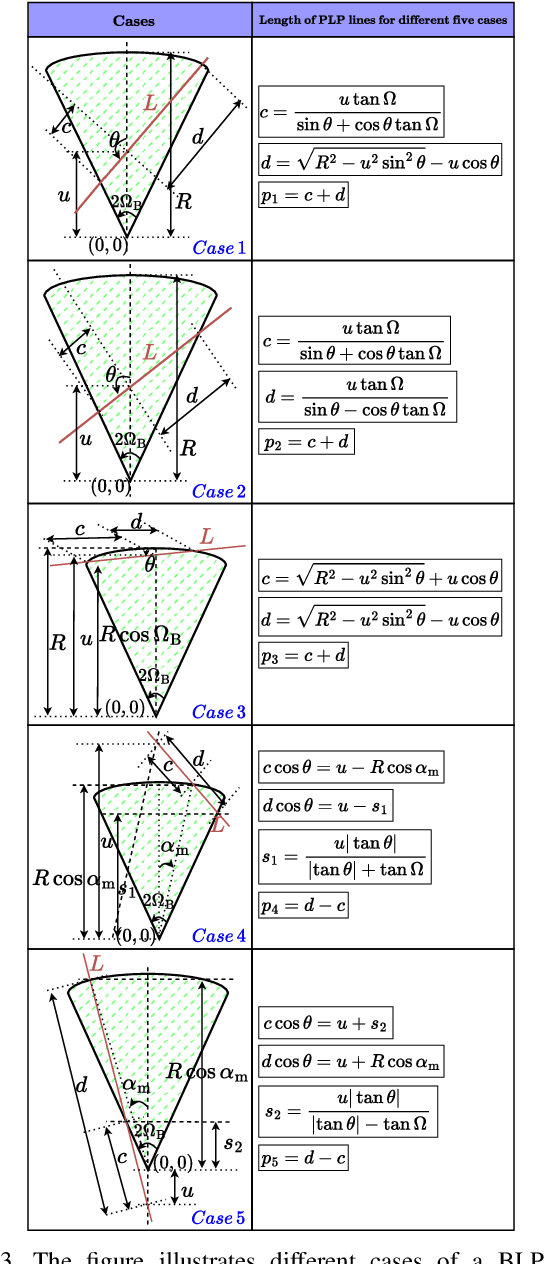
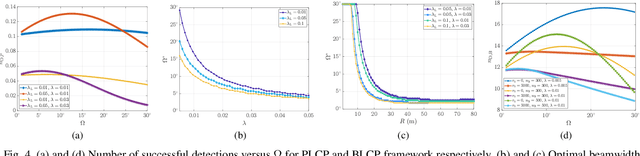
Advanced driver assistance systems (ADAS) enabled by automotive radars have significantly enhanced vehicle safety and driver experience. However, the extensive use of radars in dense road conditions introduces mutual interference, which degrades detection accuracy and reliability. Traditional interference models are limited to simple highway scenarios and cannot characterize the performance of automotive radars in dense urban environments. In our prior work, we employed stochastic geometry (SG) to develop two automotive radar network models: the Poisson line Cox process (PLCP) for dense city centers and smaller urban zones and the binomial line Cox process (BLCP) to encompass both urban cores and suburban areas. In this work, we introduce the meta-distribution (MD) framework upon these two models to distinguish the sources of variability in radar detection metrics. Additionally, we optimize the radar beamwidth and transmission probability to maximize the number of successful detections of a radar node in the network. Further, we employ a computationally efficient Chebyshev-Markov (CM) bound method for reconstructing MDs, achieving higher accuracy than the conventional Gil-Pelaez theorem. Using the framework, we analyze the specific impacts of beamwidth, detection range, and interference on radar detection performance and offer practical insights for developing adaptive radar systems tailored to diverse traffic and environmental conditions.

Impact of Urban Street Geometry on the Detection Probability of Automotive Radars

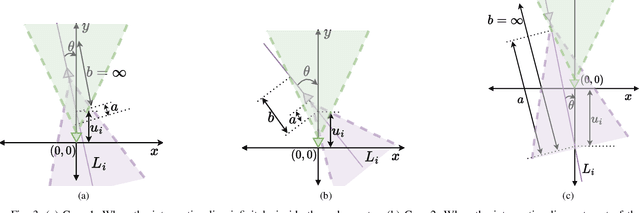
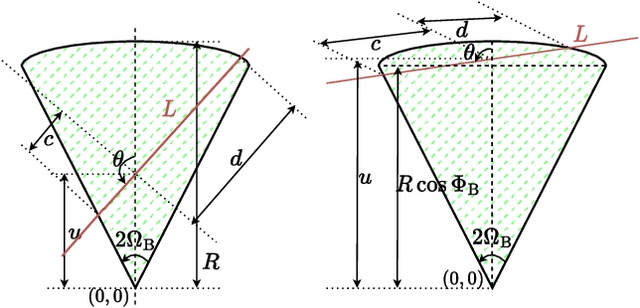
Prior works have analyzed the performance of millimeter wave automotive radars in the presence of diverse clutter and interference scenarios using stochastic geometry tools instead of more time-consuming measurement studies or system-level simulations. In these works, the distributions of radars or discrete clutter scatterers were modeled as Poisson point processes in the Euclidean space. However, since most automotive radars are likely to be mounted on vehicles and road infrastructure, road geometries are an important factor that must be considered. Instead of considering each road geometry as an individual case for study, in this work, we model each case as a specific instance of an underlying Poisson line process and further model the distribution of vehicles on the road as a Poisson point process - forming a Poisson line Cox process. Then, through the use of stochastic geometry tools, we estimate the average number of interfering radars for specific road and vehicular densities and the effect of radar parameters such as noise and beamwidth on the radar detection metrics. The numerical results are validated with Monte Carlo simulations.