Fine Grained Analysis and Optimization of Large Scale Automotive Radar Networks
Paper and Code
Nov 30, 2024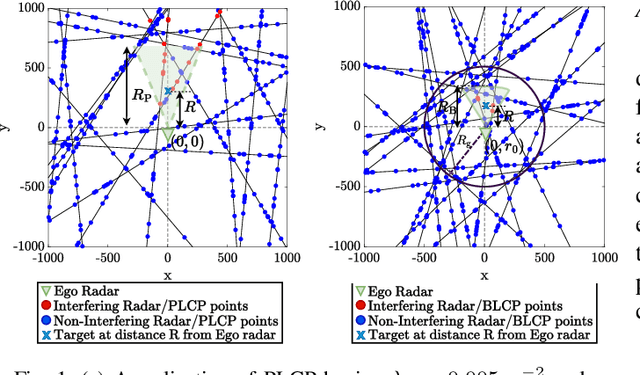
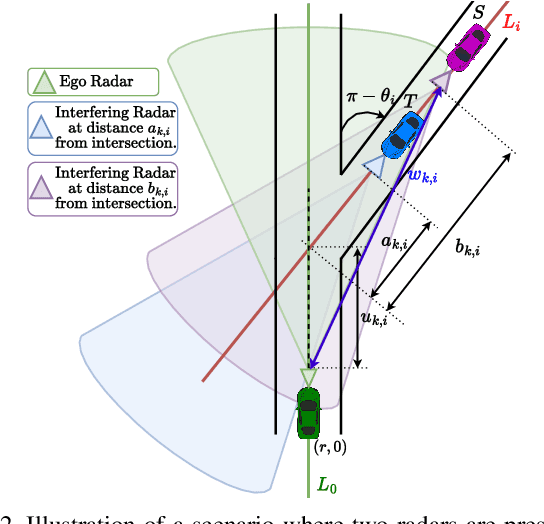
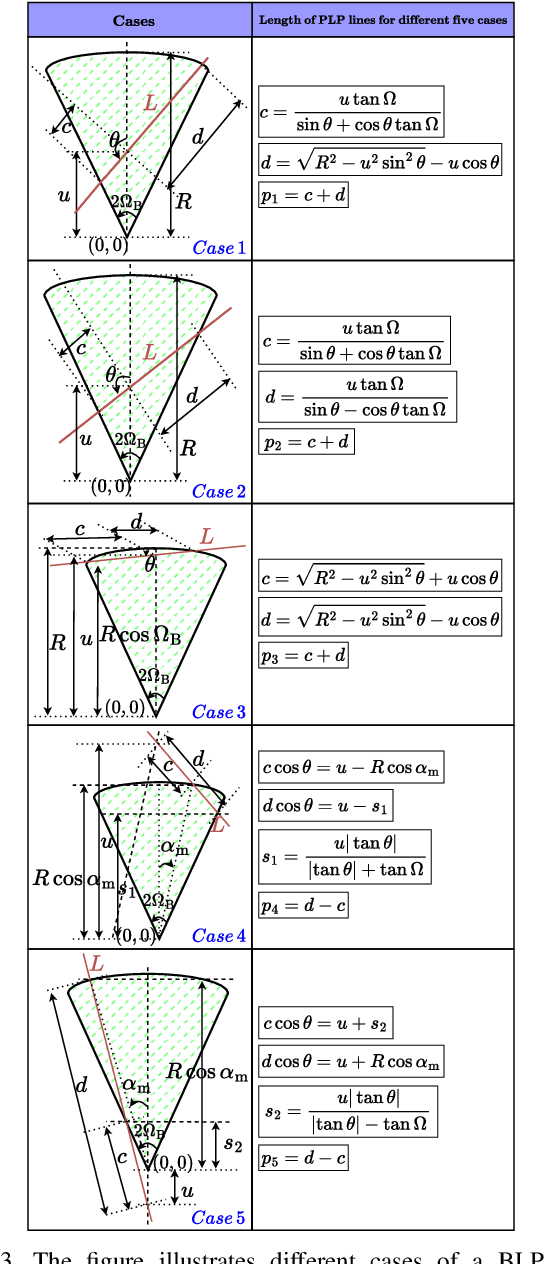
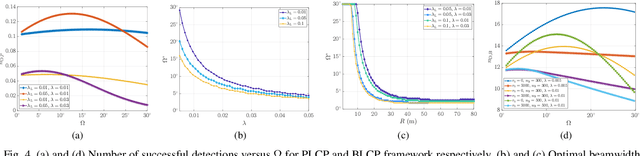
Advanced driver assistance systems (ADAS) enabled by automotive radars have significantly enhanced vehicle safety and driver experience. However, the extensive use of radars in dense road conditions introduces mutual interference, which degrades detection accuracy and reliability. Traditional interference models are limited to simple highway scenarios and cannot characterize the performance of automotive radars in dense urban environments. In our prior work, we employed stochastic geometry (SG) to develop two automotive radar network models: the Poisson line Cox process (PLCP) for dense city centers and smaller urban zones and the binomial line Cox process (BLCP) to encompass both urban cores and suburban areas. In this work, we introduce the meta-distribution (MD) framework upon these two models to distinguish the sources of variability in radar detection metrics. Additionally, we optimize the radar beamwidth and transmission probability to maximize the number of successful detections of a radar node in the network. Further, we employ a computationally efficient Chebyshev-Markov (CM) bound method for reconstructing MDs, achieving higher accuracy than the conventional Gil-Pelaez theorem. Using the framework, we analyze the specific impacts of beamwidth, detection range, and interference on radar detection performance and offer practical insights for developing adaptive radar systems tailored to diverse traffic and environmental conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge