Realistic Hair Simulation Using Image Blending

In this presented work, we propose a realistic hair simulator using image blending for dermoscopic images. This hair simulator can be used for benchmarking and validation of the hair removal methods and in data augmentation for improving computer aided diagnostic tools. We adopted one of the popular implementation of image blending to superimpose realistic hair masks to hair lesion. This method was able to produce realistic hair masks according to a predefined mask for hair. Thus, the produced hair images and masks can be used as ground truth for hair segmentation and removal methods by inpainting hair according to a pre-defined hair masks on hairfree areas. Also, we achieved a realism score equals to 1.65 in comparison to 1.59 for the state-of-the-art hair simulator.

On the Worst-case Communication Overhead for Distributed Data Shuffling

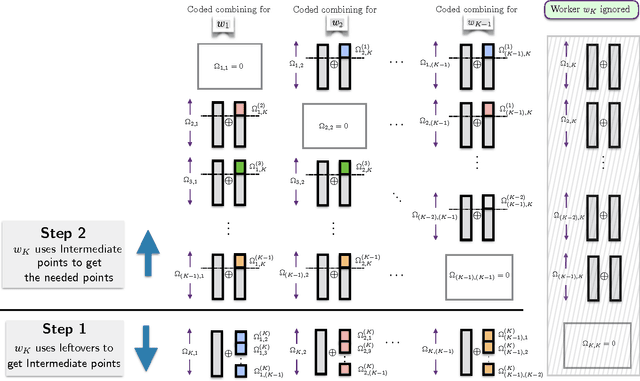
Distributed learning platforms for processing large scale data-sets are becoming increasingly prevalent. In typical distributed implementations, a centralized master node breaks the data-set into smaller batches for parallel processing across distributed workers to achieve speed-up and efficiency. Several computational tasks are of sequential nature, and involve multiple passes over the data. At each iteration over the data, it is common practice to randomly re-shuffle the data at the master node, assigning different batches for each worker to process. This random re-shuffling operation comes at the cost of extra communication overhead, since at each shuffle, new data points need to be delivered to the distributed workers. In this paper, we focus on characterizing the information theoretically optimal communication overhead for the distributed data shuffling problem. We propose a novel coded data delivery scheme for the case of no excess storage, where every worker can only store the assigned data batches under processing. Our scheme exploits a new type of coding opportunity and is applicable to any arbitrary shuffle, and for any number of workers. We also present an information theoretic lower bound on the minimum communication overhead for data shuffling, and show that the proposed scheme matches this lower bound for the worst-case communication overhead.

Information Theoretic Limits of Data Shuffling for Distributed Learning

Data shuffling is one of the fundamental building blocks for distributed learning algorithms, that increases the statistical gain for each step of the learning process. In each iteration, different shuffled data points are assigned by a central node to a distributed set of workers to perform local computations, which leads to communication bottlenecks. The focus of this paper is on formalizing and understanding the fundamental information-theoretic trade-off between storage (per worker) and the worst-case communication overhead for the data shuffling problem. We completely characterize the information theoretic trade-off for $K=2$, and $K=3$ workers, for any value of storage capacity, and show that increasing the storage across workers can reduce the communication overhead by leveraging coding. We propose a novel and systematic data delivery and storage update strategy for each data shuffle iteration, which preserves the structural properties of the storage across the workers, and aids in minimizing the communication overhead in subsequent data shuffling iterations.