Maximum Selection and Ranking under Noisy Comparisons

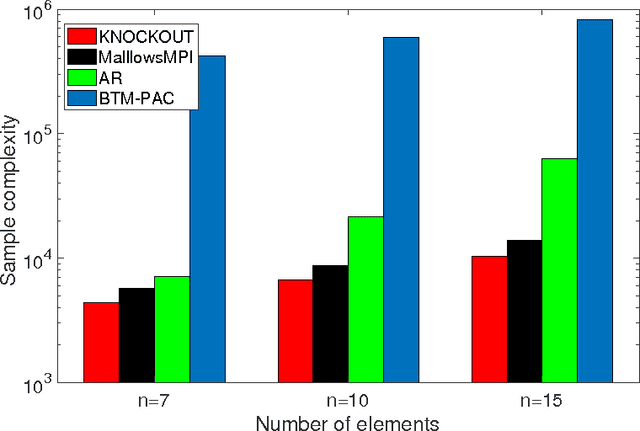
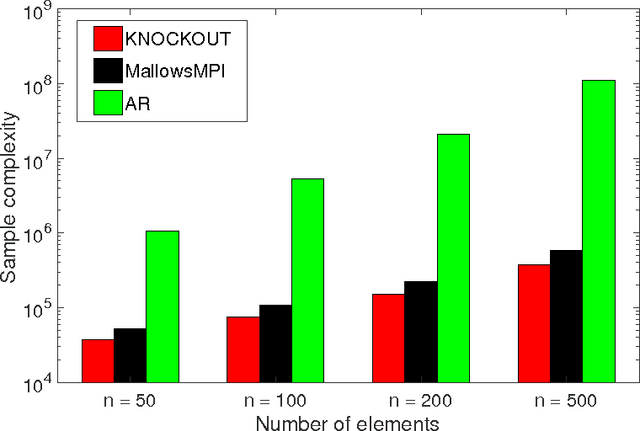
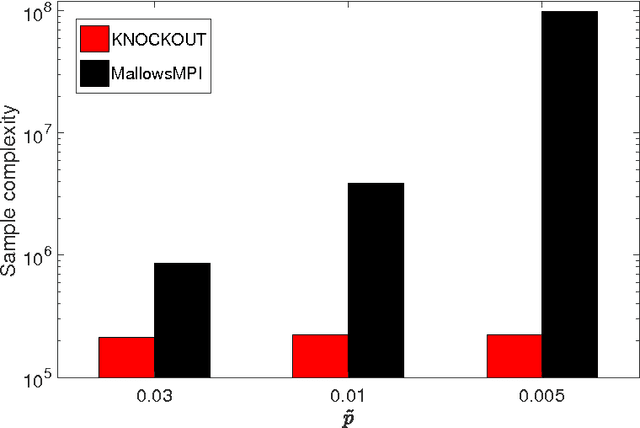
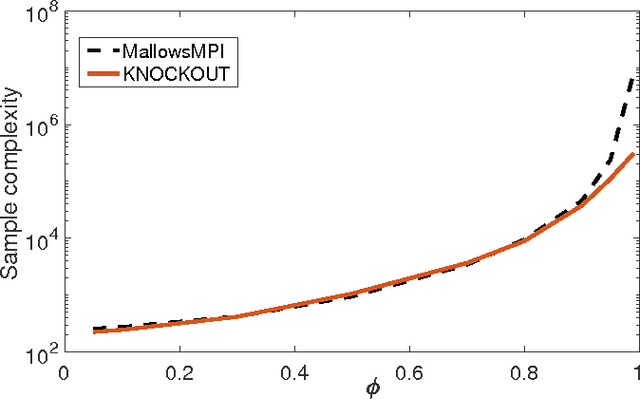
We consider $(\epsilon,\delta)$-PAC maximum-selection and ranking for general probabilistic models whose comparisons probabilities satisfy strong stochastic transitivity and stochastic triangle inequality. Modifying the popular knockout tournament, we propose a maximum-selection algorithm that uses $\mathcal{O}\left(\frac{n}{\epsilon^2}\log \frac{1}{\delta}\right)$ comparisons, a number tight up to a constant factor. We then derive a general framework that improves the performance of many ranking algorithms, and combine it with merge sort and binary search to obtain a ranking algorithm that uses $\mathcal{O}\left(\frac{n\log n (\log \log n)^3}{\epsilon^2}\right)$ comparisons for any $\delta\ge\frac1n$, a number optimal up to a $(\log \log n)^3$ factor.

Faster Algorithms for Testing under Conditional Sampling

There has been considerable recent interest in distribution-tests whose run-time and sample requirements are sublinear in the domain-size $k$. We study two of the most important tests under the conditional-sampling model where each query specifies a subset $S$ of the domain, and the response is a sample drawn from $S$ according to the underlying distribution. For identity testing, which asks whether the underlying distribution equals a specific given distribution or $\epsilon$-differs from it, we reduce the known time and sample complexities from $\tilde{\mathcal{O}}(\epsilon^{-4})$ to $\tilde{\mathcal{O}}(\epsilon^{-2})$, thereby matching the information theoretic lower bound. For closeness testing, which asks whether two distributions underlying observed data sets are equal or different, we reduce existing complexity from $\tilde{\mathcal{O}}(\epsilon^{-4} \log^5 k)$ to an even sub-logarithmic $\tilde{\mathcal{O}}(\epsilon^{-5} \log \log k)$ thus providing a better bound to an open problem in Bertinoro Workshop on Sublinear Algorithms [Fisher, 2004].