Maximum Selection and Ranking under Noisy Comparisons
Paper and Code
May 15, 2017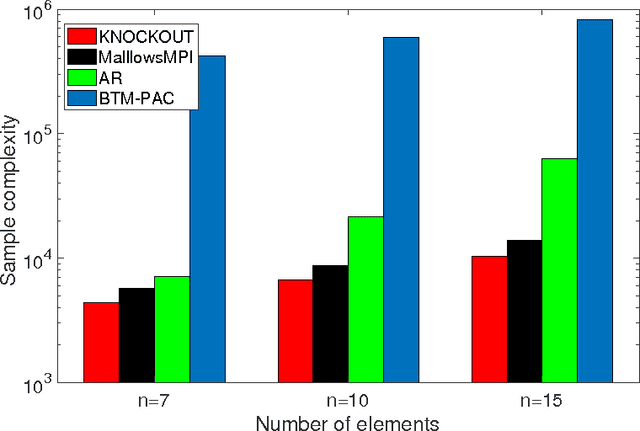
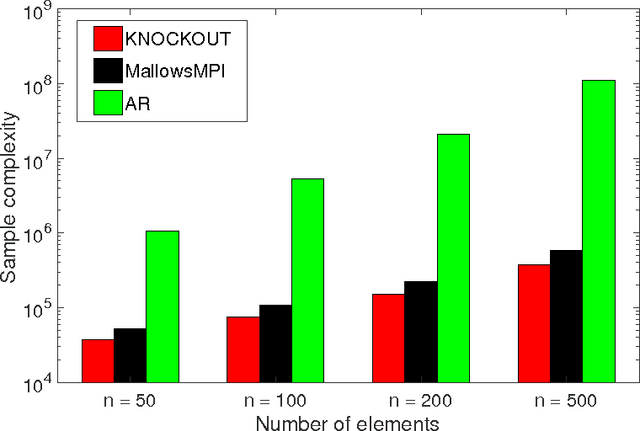
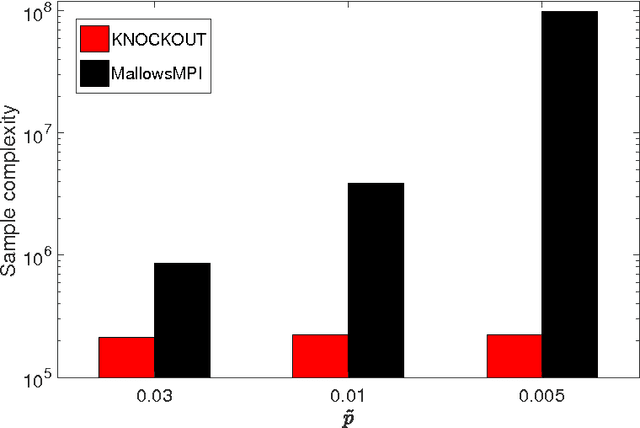
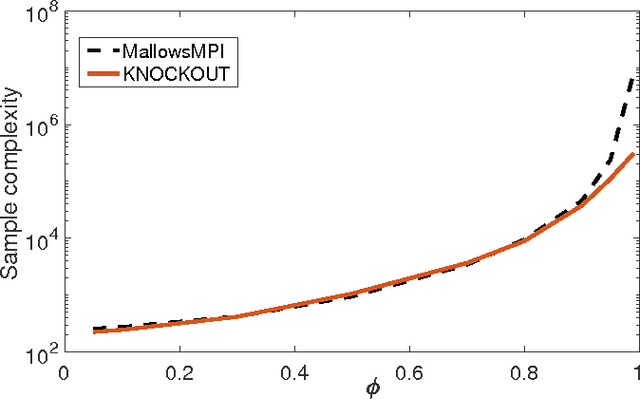
We consider $(\epsilon,\delta)$-PAC maximum-selection and ranking for general probabilistic models whose comparisons probabilities satisfy strong stochastic transitivity and stochastic triangle inequality. Modifying the popular knockout tournament, we propose a maximum-selection algorithm that uses $\mathcal{O}\left(\frac{n}{\epsilon^2}\log \frac{1}{\delta}\right)$ comparisons, a number tight up to a constant factor. We then derive a general framework that improves the performance of many ranking algorithms, and combine it with merge sort and binary search to obtain a ranking algorithm that uses $\mathcal{O}\left(\frac{n\log n (\log \log n)^3}{\epsilon^2}\right)$ comparisons for any $\delta\ge\frac1n$, a number optimal up to a $(\log \log n)^3$ factor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge