Bayesian Kernel Regression for Functional Data

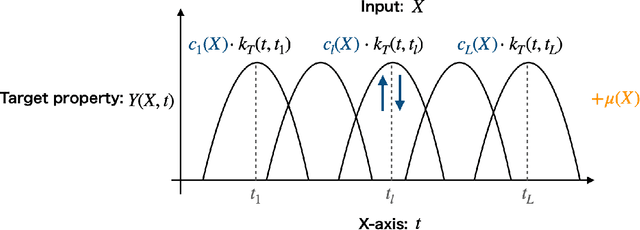
In supervised learning, the output variable to be predicted is often represented as a function, such as a spectrum or probability distribution. Despite its importance, functional output regression remains relatively unexplored. In this study, we propose a novel functional output regression model based on kernel methods. Unlike conventional approaches that independently train regressors with scalar outputs for each measurement point of the output function, our method leverages the covariance structure within the function values, akin to multitask learning, leading to enhanced learning efficiency and improved prediction accuracy. Compared with existing nonlinear function-on-scalar models in statistical functional data analysis, our model effectively handles high-dimensional nonlinearity while maintaining a simple model structure. Furthermore, the fully kernel-based formulation allows the model to be expressed within the framework of reproducing kernel Hilbert space (RKHS), providing an analytic form for parameter estimation and a solid foundation for further theoretical analysis. The proposed model delivers a functional output predictive distribution derived analytically from a Bayesian perspective, enabling the quantification of uncertainty in the predicted function. We demonstrate the model's enhanced prediction performance through experiments on artificial datasets and density of states prediction tasks in materials science.

Shotgun crystal structure prediction using machine-learned formation energies

Stable or metastable crystal structures of assembled atoms can be predicted by finding the global or local minima of the energy surface with respect to the atomic configurations. Generally, this requires repeated first-principles energy calculations that are impractical for large systems, such as those containing more than 30 atoms in the unit cell. Here, we have made significant progress in solving the crystal structure prediction problem with a simple but powerful machine-learning workflow; using a machine-learning surrogate for first-principles energy calculations, we performed non-iterative, single-shot screening using a large library of virtually created crystal structures. The present method relies on two key technical components: transfer learning, which enables a highly accurate energy prediction of pre-relaxed crystalline states given only a small set of training samples from first-principles calculations, and generative models to create promising and diverse crystal structures for screening. Here, first-principles calculations were performed only to generate the training samples, and for the optimization of a dozen or fewer finally narrowed-down crystal structures. Our shotgun method was more than 5--10 times less computationally demanding and achieved an outstanding prediction accuracy that was 2--6 times higher than that of the conventional methods that rely heavily on iterative first-principles calculations.

Crystal structure prediction with machine learning-based element substitution

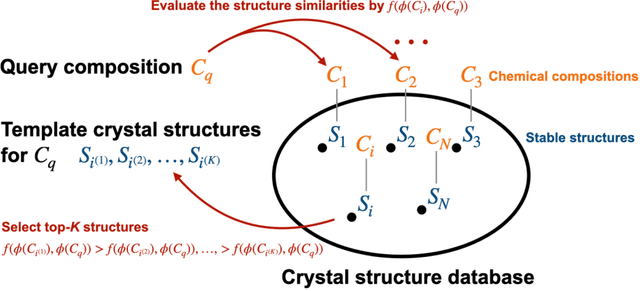
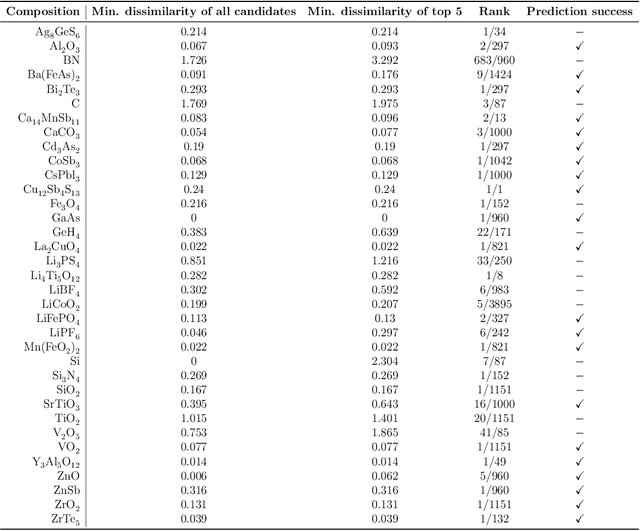
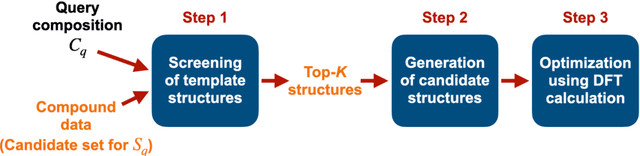
The prediction of energetically stable crystal structures formed by a given chemical composition is a central problem in solid-state physics. In principle, the crystalline state of assembled atoms can be determined by optimizing the energy surface, which in turn can be evaluated using first-principles calculations. However, performing the iterative gradient descent on the potential energy surface using first-principles calculations is prohibitively expensive for complex systems, such as those with many atoms per unit cell. Here, we present a unique methodology for crystal structure prediction (CSP) that relies on a machine learning algorithm called metric learning. It is shown that a binary classifier, trained on a large number of already identified crystal structures, can determine the isomorphism of crystal structures formed by two given chemical compositions with an accuracy of approximately 96.4\%. For a given query composition with an unknown crystal structure, the model is used to automatically select from a crystal structure database a set of template crystals with nearly identical stable structures to which element substitution is to be applied. Apart from the local relaxation calculation of the identified templates, the proposed method does not use ab initio calculations. The potential of this substation-based CSP is demonstrated for a wide variety of crystal systems.

Recreation of the Periodic Table with an Unsupervised Machine Learning Algorithm

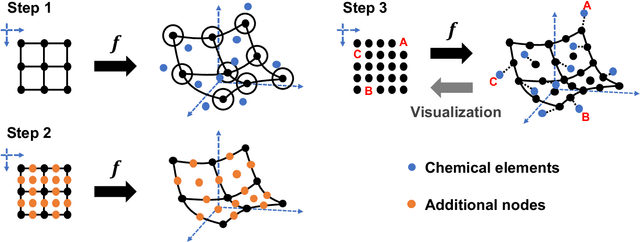
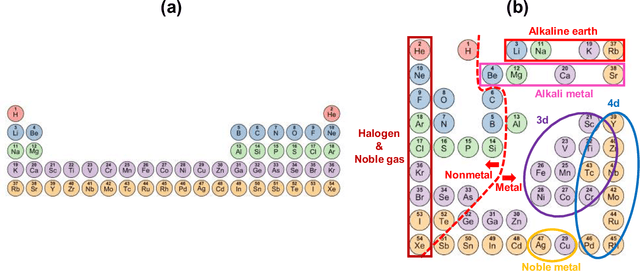
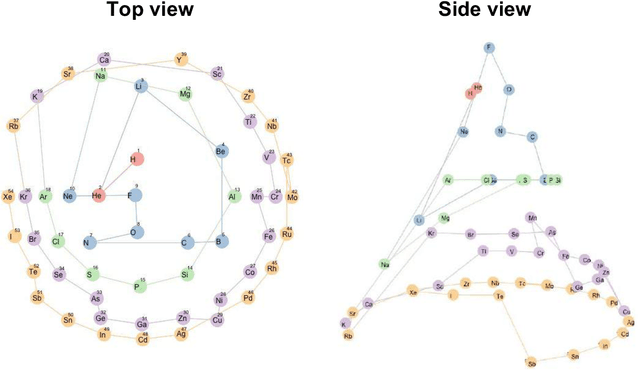
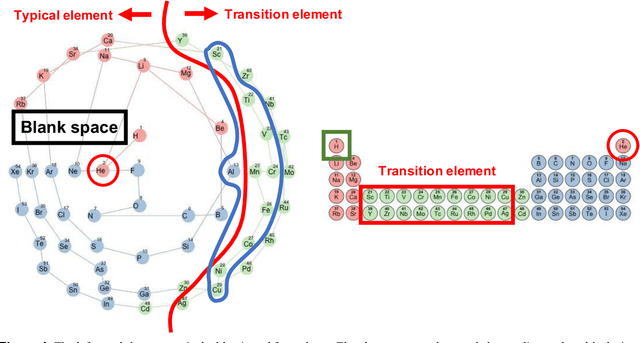
In 1869, the first draft of the periodic table was published by Russian chemist Dmitri Mendeleev. In terms of data science, his achievement can be viewed as a successful example of feature embedding based on human cognition: chemical properties of all known elements at that time were compressed onto the two-dimensional grid system for tabular display. In this study, we seek to answer the question of whether machine learning can reproduce or recreate the periodic table by using observed physicochemical properties of the elements. To achieve this goal, we developed a periodic table generator (PTG). The PTG is an unsupervised machine learning algorithm based on the generative topographic mapping (GTM), which can automate the translation of high-dimensional data into a tabular form with varying layouts on-demand. The PTG autonomously produced various arrangements of chemical symbols, which organized a two-dimensional array such as Mendeleev's periodic table or three-dimensional spiral table according to the underlying periodicity in the given data. We further showed what the PTG learned from the element data and how the element features, such as melting point and electronegativity, are compressed to the lower-dimensional latent spaces.