Quantized Phase Alignment by Discrete Phase Shifts for Reconfigurable Intelligent Surface-Assisted Communication Systems

Reconfigurable intelligent surface (RIS) has aroused a surge of interest in recent years. In this paper, we investigate the joint phase alignment and phase quantization on discrete phase shift designs for RIS-assisted single-input single-output (SISO) system. Firstly, the phenomena of phase distribution in far field and near field are respectively unveiled, paving the way for discretization of phase shift for RIS. Then, aiming at aligning phases, the phase distribution law and its underlying degree-of-freedom (DoF) are characterized, serving as the guideline of phase quantization strategies. Subsequently, two phase quantization methods, dynamic threshold phase quantization (DTPQ) and equal interval phase quantization (EIPQ), are proposed to strengthen the beamforming effect of RIS. DTPQ is capable of calculating the optimal discrete phase shifts with linear complexity in the number of unit cells on RIS, whilst EIPQ is a simplified method with a constant complexity yielding sub-optimal solution. Simulation results demonstrate that both methods achieve substantial improvements on power gain, stability, and robustness over traditional quantization methods. The path loss (PL) scaling law under discrete phase shift of RIS is unveiled for the first time, with the phase shifts designed by DTPQ due to its optimality. Additionally, the field trials conducted at 2.6 GHz and 35 GHz validate the favourable performance of the proposed methods in practical communication environment.

AI Uncertainty Based on Rademacher Complexity and Shannon Entropy

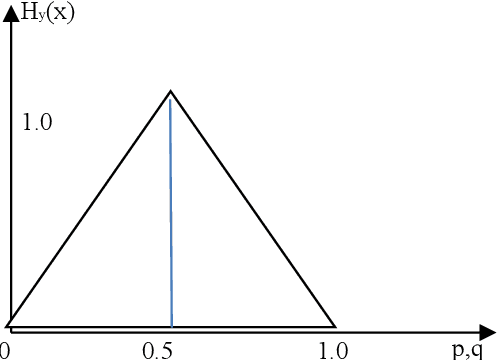
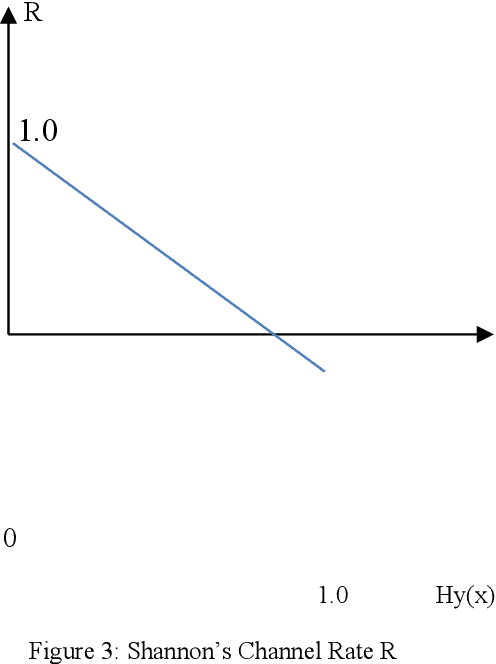
In this paper from communication channel coding perspective we are able to present both a theoretical and practical discussion of AI's uncertainty, capacity and evolution for pattern classification based on the classical Rademacher complexity and Shannon entropy. First AI capacity is defined as in communication channels. It is shown qualitatively that the classical Rademacher complexity and Shannon entropy used in communication theory is closely related by their definitions, given a pattern classification problem with a complexity measured by Rademacher complexity. Secondly based on the Shannon mathematical theory on communication coding, we derive several sufficient and necessary conditions for an AI's error rate approaching zero in classifications problems. A 1/2 criteria on Shannon entropy is derived in this paper so that error rate can approach zero or is zero for AI pattern classification problems. Last but not least, we show our analysis and theory by providing examples of AI pattern classifications with error rate approaching zero or being zero.

A Theory on AI Uncertainty Based on Rademacher Complexity and Shannon Entropy

In this paper, we present a theoretical discussion on AI deep learning neural network uncertainty investigation based on the classical Rademacher complexity and Shannon entropy. First it is shown that the classical Rademacher complexity and Shannon entropy is closely related by quantity by definitions. Secondly based on the Shannon mathematical theory on communication [3], we derive a criteria to ensure AI correctness and accuracy in classifications problems. Last but not the least based on Peter Barlette's work, we show both a relaxing condition and a stricter condition to guarantee the correctness and accuracy in AI classification . By elucidating in this paper criteria condition in terms of Shannon entropy based on Shannon theory, it becomes easier to explore other criteria in terms of other complexity measurements such as Vapnik-Cheronenkis, Gaussian complexity by taking advantage of the relations studies results in other references. A close to 0.5 criteria on Shannon entropy is derived in this paper for the theoretical investigation of AI accuracy and correctness for classification problems.

Electrical Impedance Tomography based on Genetic Algorithm

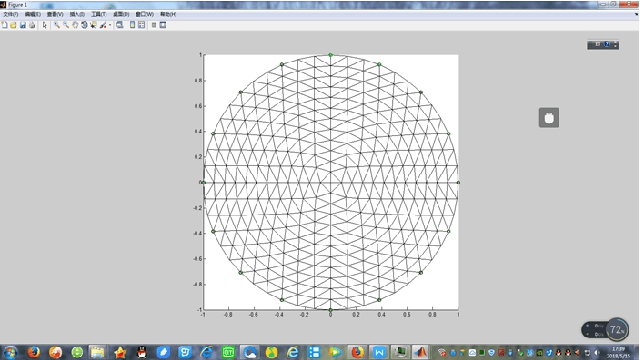
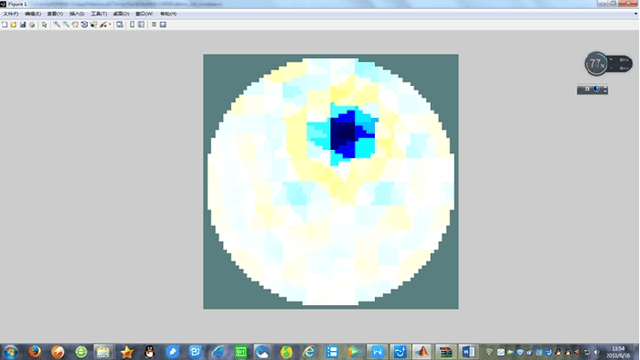
In this paper, we applies GA algorithm into Electrical Impedance Tomography (EIT) application. We first outline the EIT problem as an optimization problem and define a target optimization function. Then we show how the GA algorithm as an alternative searching algorithm can be used for solving EIT inverse problem. In this paper, we explore evolutionary methods such as GA algorithms combined with various regularization operators to solve EIT inverse computing problem. Key words: Electrical Impedance Tomography (EIT), GA, Tikhonov operator , Mumford-Shah operator, Particle Swarm Optimization(PSO), Back Propagation(BP).