AI Uncertainty Based on Rademacher Complexity and Shannon Entropy
Paper and Code
Feb 12, 2021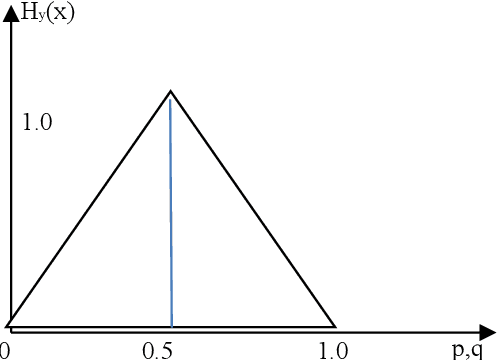
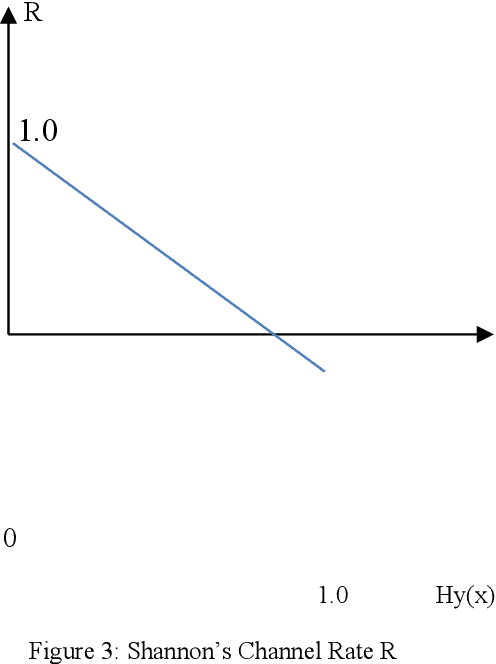
In this paper from communication channel coding perspective we are able to present both a theoretical and practical discussion of AI's uncertainty, capacity and evolution for pattern classification based on the classical Rademacher complexity and Shannon entropy. First AI capacity is defined as in communication channels. It is shown qualitatively that the classical Rademacher complexity and Shannon entropy used in communication theory is closely related by their definitions, given a pattern classification problem with a complexity measured by Rademacher complexity. Secondly based on the Shannon mathematical theory on communication coding, we derive several sufficient and necessary conditions for an AI's error rate approaching zero in classifications problems. A 1/2 criteria on Shannon entropy is derived in this paper so that error rate can approach zero or is zero for AI pattern classification problems. Last but not least, we show our analysis and theory by providing examples of AI pattern classifications with error rate approaching zero or being zero.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge