Multi-view Clustering via Unified Multi-kernel Learning and Matrix Factorization

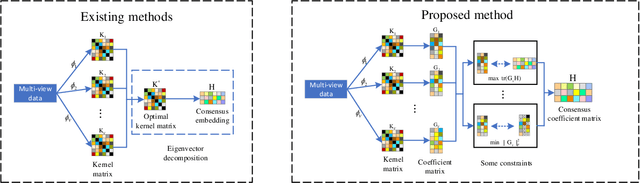
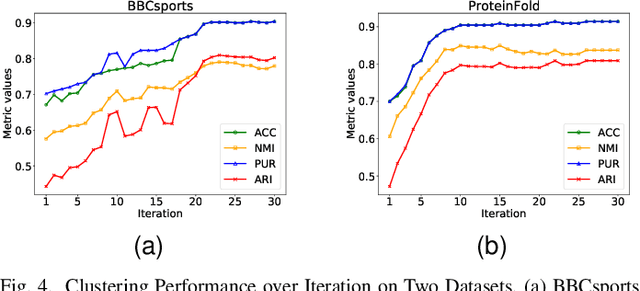
Multi-view clustering has become increasingly important due to the multi-source character of real-world data. Among existing multi-view clustering methods, multi-kernel clustering and matrix factorization-based multi-view clustering have gained widespread attention as mainstream approaches. However, multi-kernel clustering tends to learn an optimal kernel and then perform eigenvalue decomposition on it, which leads to high computational complexity. Matrix factorization-based multi-view clustering methods impose orthogonal constraints on individual views. This overly emphasizes the accuracy of clustering structures within single views and restricts the learning of individual views. Based on this analysis, we propose a multi-view clustering method that integrates multi-kernel learning with matrix factorization. This approach combines the advantages of both multi-kernel learning and matrix factorization. It removes the orthogonal constraints on individual views and imposes orthogonal constraints on the consensus matrix, resulting in an accurate final clustering structure. Ultimately, the method is unified into a simple form of multi-kernel clustering, but avoids learning an optimal kernel, thus reducing the time complexity. Furthermore, we propose an efficient three-step optimization algorithm to achieve a locally optimal solution. Experiments on widely-used real-world datasets demonstrate the effectiveness of our proposed method.

GFDC: A Granule Fusion Density-Based Clustering with Evidential Reasoning

Currently, density-based clustering algorithms are widely applied because they can detect clusters with arbitrary shapes. However, they perform poorly in measuring global density, determining reasonable cluster centers or structures, assigning samples accurately and handling data with large density differences among clusters. To overcome their drawbacks, this paper proposes a granule fusion density-based clustering with evidential reasoning (GFDC). Both local and global densities of samples are measured by a sparse degree metric first. Then information granules are generated in high-density and low-density regions, assisting in processing clusters with significant density differences. Further, three novel granule fusion strategies are utilized to combine granules into stable cluster structures, helping to detect clusters with arbitrary shapes. Finally, by an assignment method developed from Dempster-Shafer theory, unstable samples are assigned. After using GFDC, a reasonable clustering result and some identified outliers can be obtained. The experimental results on extensive datasets demonstrate the effectiveness of GFDC.

Knowledge reduction of dynamic covering decision information systems with varying attribute values

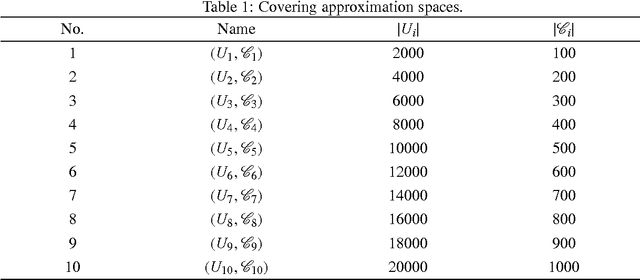
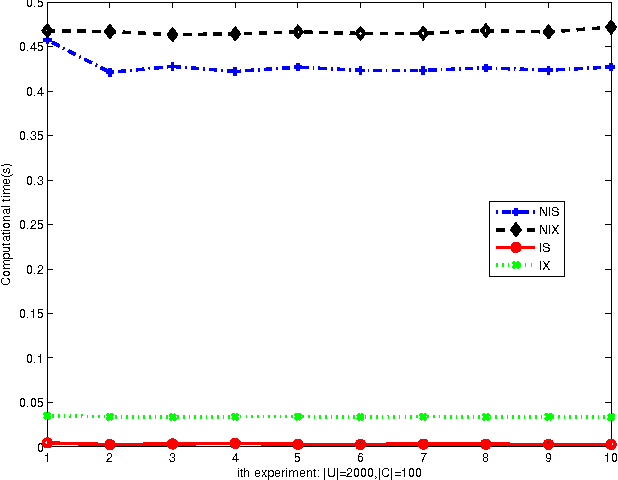
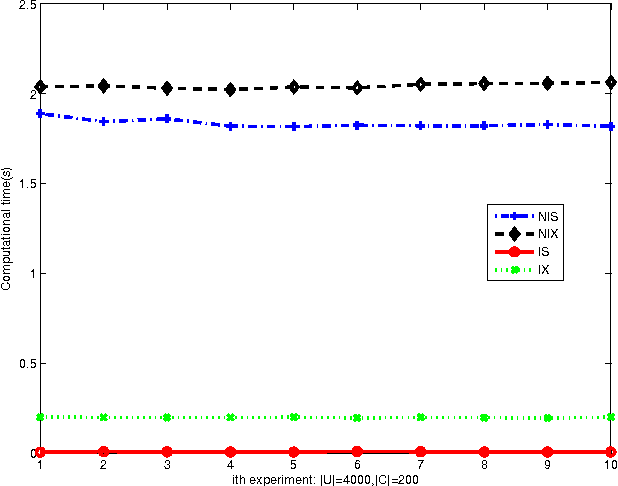
Knowledge reduction of dynamic covering information systems involves with the time in practical situations. In this paper, we provide incremental approaches to computing the type-1 and type-2 characteristic matrices of dynamic coverings because of varying attribute values. Then we present incremental algorithms of constructing the second and sixth approximations of sets by using characteristic matrices. We employ experimental results to illustrate that the incremental approaches are effective to calculate approximations of sets in dynamic covering information systems. Finally, we perform knowledge reduction of dynamic covering information systems with the incremental approaches.