Multi-task CNN Behavioral Embedding Model For Transaction Fraud Detection

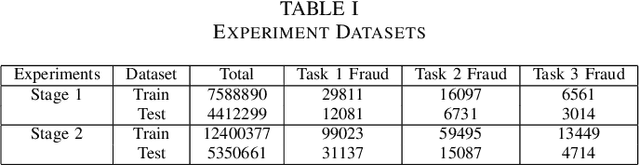
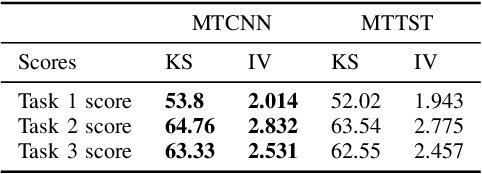
The burgeoning e-Commerce sector requires advanced solutions for the detection of transaction fraud. With an increasing risk of financial information theft and account takeovers, deep learning methods have become integral to the embedding of behavior sequence data in fraud detection. However, these methods often struggle to balance modeling capabilities and efficiency and incorporate domain knowledge. To address these issues, we introduce the multitask CNN behavioral Embedding Model for Transaction Fraud Detection. Our contributions include 1) introducing a single-layer CNN design featuring multirange kernels which outperform LSTM and Transformer models in terms of scalability and domain-focused inductive bias, and 2) the integration of positional encoding with CNN to introduce sequence-order signals enhancing overall performance, and 3) implementing multitask learning with randomly assigned label weights, thus removing the need for manual tuning. Testing on real-world data reveals our model's enhanced performance of downstream transaction models and comparable competitiveness with the Transformer Time Series (TST) model.

Variational Langevin Hamiltonian Monte Carlo for Distant Multi-modal Sampling

The Hamiltonian Monte Carlo (HMC) sampling algorithm exploits Hamiltonian dynamics to construct efficient Markov Chain Monte Carlo (MCMC), which has become increasingly popular in machine learning and statistics. Since HMC uses the gradient information of the target distribution, it can explore the state space much more efficiently than the random-walk proposals. However, probabilistic inference involving multi-modal distributions is very difficult for standard HMC method, especially when the modes are far away from each other. Sampling algorithms are then often incapable of traveling across the places of low probability. In this paper, we propose a novel MCMC algorithm which aims to sample from multi-modal distributions effectively. The method improves Hamiltonian dynamics to reduce the autocorrelation of the samples and uses a variational distribution to explore the phase space and find new modes. A formal proof is provided which shows that the proposed method can converge to target distributions. Both synthetic and real datasets are used to evaluate its properties and performance. The experimental results verify the theory and show superior performance in multi-modal sampling.