Motion Planning of a Spin-Rolling Sphere on a Plane

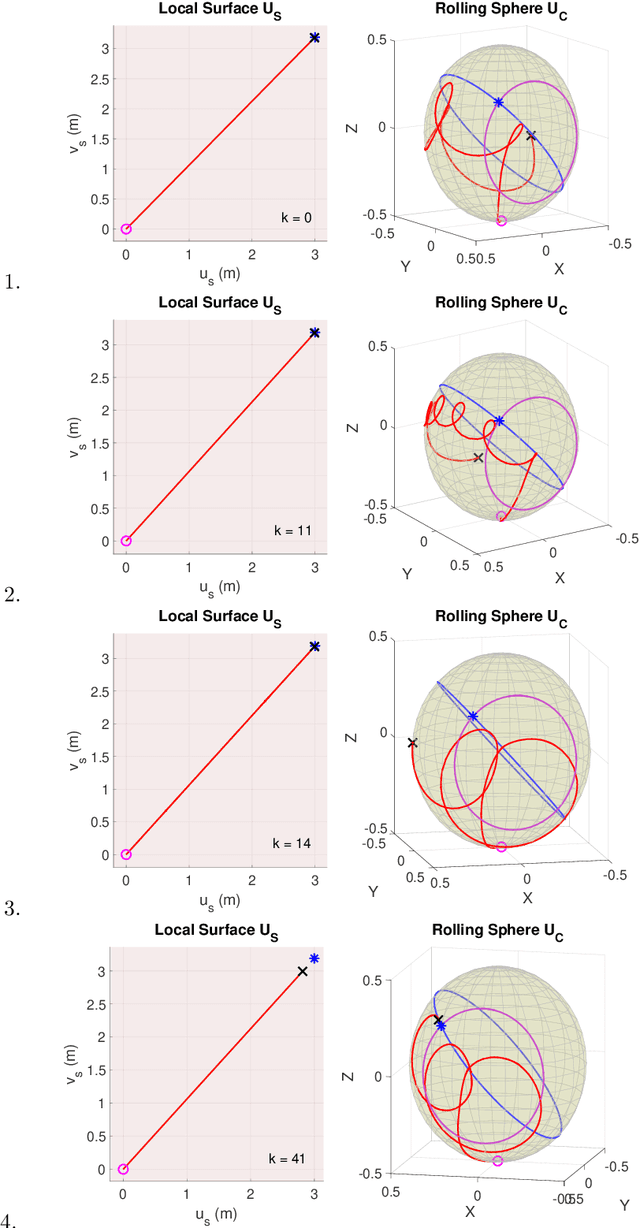
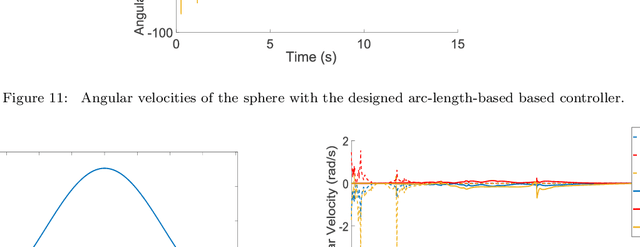
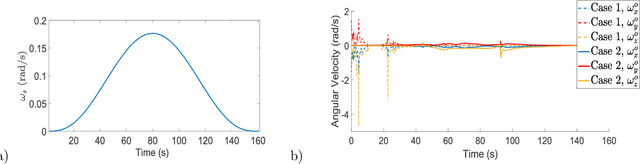
The paper deals with motion planning for a spin-rolling sphere when the sphere follows a straight path on a plane. Since the motion of the sphere is constrained by the straight line, the control of the sphere's spin motion is essential to converge to a desired configuration of the sphere. In this paper, we show a new geometric-based planning approach that is based on a full-state description of this nonlinear system. First, the problem statement of the motion planning is posed. Next, we develop a geometric controller implemented as a virtual surface by using the Darboux frame kinematics. This virtual surface generates arc-length-based inputs for controlling the trajectories of the sphere. Then, an iterative algorithm is designed to tune these inputs for the desired configurations. The feasibility of the proposed approach is verified by simulations.

Darboux-Frame-Based Parametrization for a Spin-Rolling Sphere on a Plane: A Nonlinear Transformation of Underactuated System to Fully-Actuated Model

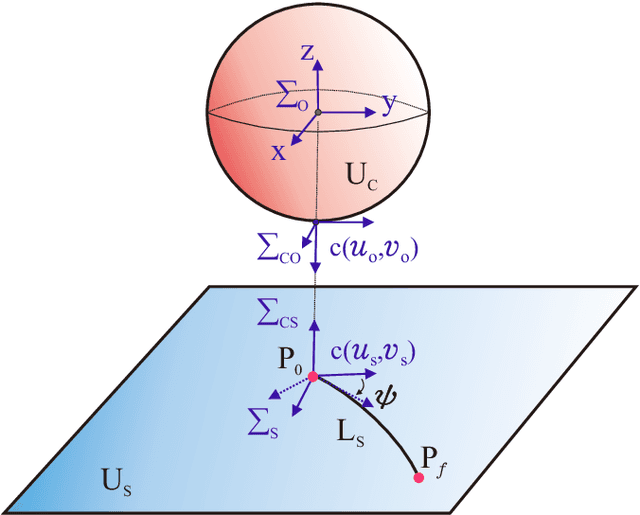
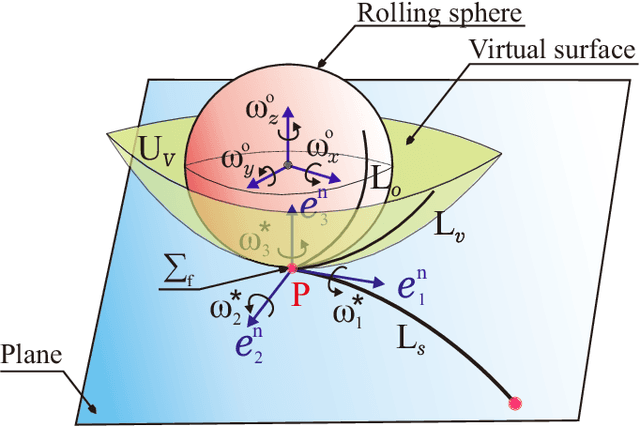
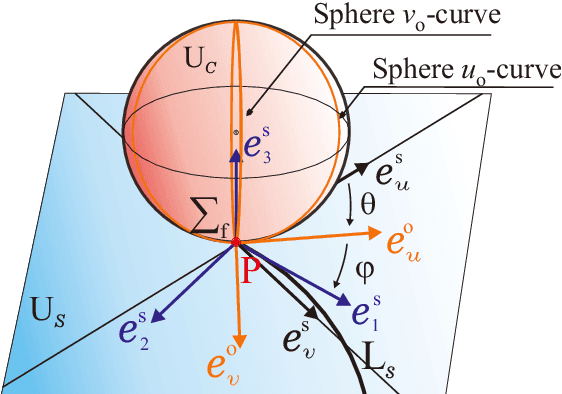
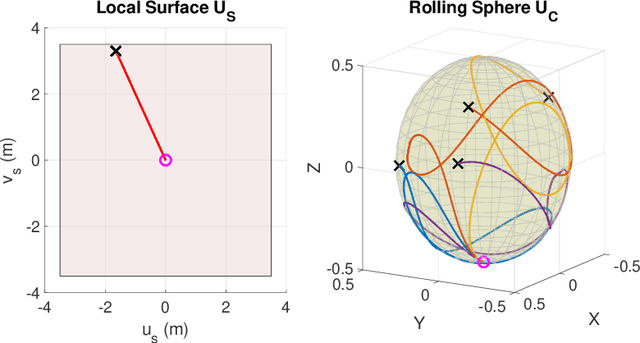
This paper presents a new kinematic model based on the Darboux-frame for motion control and planning. In this work, we show that an underactuated system as a spin-rolling sphere on a plane with three inputs and five states can be transformed into a fully-actuated model by the given Darboux-frame transformation. This nonlinear state transformation is a geometric model that is different from conventional state-space models. First, a kinematic model of the Darboux frame at the contact point of a rotating object i.e., the sphere, is established. Next, we propose a virtual surface that is trapped between sphere and plane surfaces. This virtual surface generates arc-length-based inputs for controlling the trajectories on the sphere and plane. Finally, we discuss the controllability of this new system after our introduced transformation. In the future, we will design a proper geometric path planning method for the obtained kinematic model.

Singularity-Free Inverse Dynamics for Underactuated Systems with a Rotating Mass

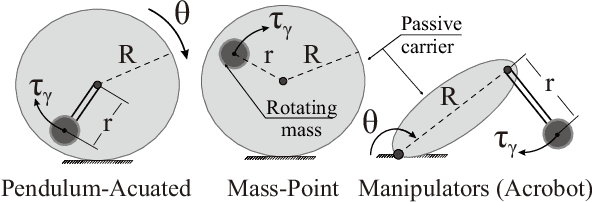
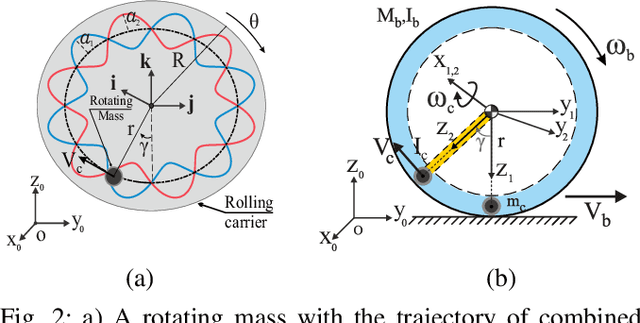
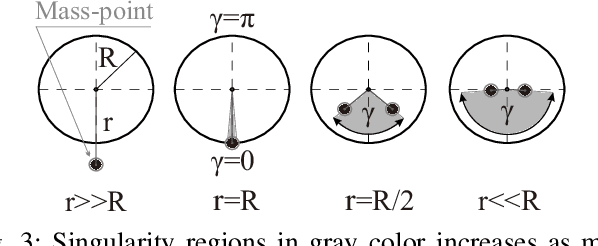
Motion control of underactuated systems through the inverse dynamics contains configuration singularities. These limitations in configuration space mainly stem from the inertial coupling that passive joints/bodies create. In this study, we present a model that is free from singularity while the trajectory of the rotating mass has a small-amplitude sine wave around its circle. First, we derive the modified non-linear dynamics for a rolling system. Also, the singularity regions for this underactuated system is demonstrated. Then, the wave parameters are designed under certain conditions to remove the coupling singularities. We obtain these conditions from the positive definiteness of the inertia matrix in the inverse dynamics. Finally, the simulation results are confirmed by using a prescribed Beta function on the specified states of the rolling carrier. Because our algebraic method is integrated into the non-linear dynamics, the proposed solution has a great potential to be extended to the Lagrangian mechanics with multiple degrees-of-freedom.

Dynamical Behavior Investigation and Analysis of Novel Mechanism for Simulated Spherical Robot named "RollRoller"

This paper introduces a simulation study of fluid actuated multi-driven closed system as spherical mobile robot called "RollRoller". Robot's mechanism design consists of two essential parts: tubes to lead a core and mechanical controlling parts to correspond movements. Our robot gets its motivation force by displacing the spherical movable mass known as core in curvy manners inside certain pipes. This simulation investigates by explaining the mechanical and structural features of the robot for creating hydraulic-base actuation via force and momentum analysis. Next, we categorize difficult and integrated 2D motions to omit unstable equilibrium points through derived nonlinear dynamics. We propose an algorithmic position control in forward direction that creates hybrid model as solution for motion planning problem in spherical robot. By deriving nonlinear dynamics of the spherical robot and implementing designed motion planning, we show how RollRoller can be efficient in high speed movements in comparison to the other pendulum-driven models. Then, we validate the results of this position control obtained by nonlinear dynamics via Adams/view simulation which uses the imported solid model of RollRoller. Lastly, We have a look to the circular maneuver of this robot by the same simulator.