Singularity-Free Inverse Dynamics for Underactuated Systems with a Rotating Mass
Paper and Code
Feb 21, 2020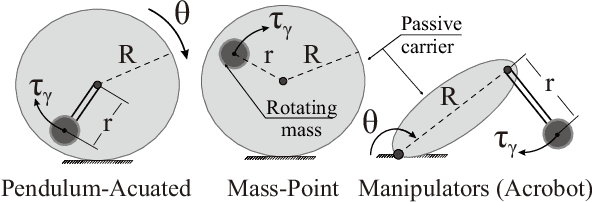
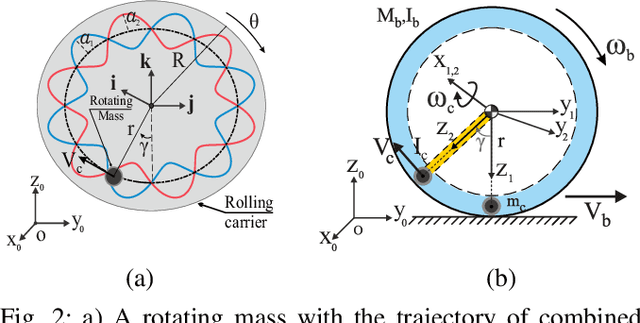
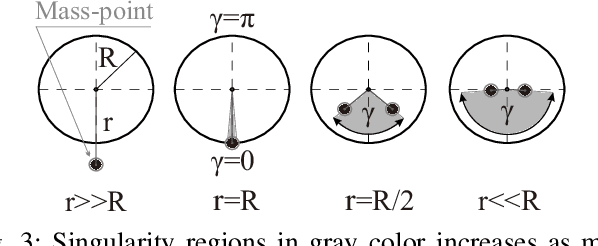

Motion control of underactuated systems through the inverse dynamics contains configuration singularities. These limitations in configuration space mainly stem from the inertial coupling that passive joints/bodies create. In this study, we present a model that is free from singularity while the trajectory of the rotating mass has a small-amplitude sine wave around its circle. First, we derive the modified non-linear dynamics for a rolling system. Also, the singularity regions for this underactuated system is demonstrated. Then, the wave parameters are designed under certain conditions to remove the coupling singularities. We obtain these conditions from the positive definiteness of the inertia matrix in the inverse dynamics. Finally, the simulation results are confirmed by using a prescribed Beta function on the specified states of the rolling carrier. Because our algebraic method is integrated into the non-linear dynamics, the proposed solution has a great potential to be extended to the Lagrangian mechanics with multiple degrees-of-freedom.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge