Mikhail Soutchanski
Ryerson University
Planning as Theorem Proving with Heuristics
Apr 01, 2023Abstract:Planning as theorem proving in situation calculus was abandoned 50 years ago as an impossible project. But we have developed a Theorem Proving Lifted Heuristic (TPLH) planner that searches for a plan in a tree of situations using the A* search algorithm. It is controlled by a delete relaxation-based domain independent heuristic. We compare TPLH with Fast Downward (FD) and Best First Width Search (BFWS) planners over several standard benchmarks. Since our implementation of the heuristic function is not optimized, TPLH is slower than FD and BFWS. But it computes shorter plans, and it explores fewer states. We discuss previous research on planning within KR\&R and identify related directions. Thus, we show that deductive lifted heuristic planning in situation calculus is actually doable.
A Logical Semantics for PDDL+
Nov 23, 2021

Abstract:PDDL+ is an extension of PDDL2.1 which incorporates fully-featured autonomous processes and allows for better modelling of mixed discrete-continuous domains. Unlike PDDL2.1, PDDL+ lacks a logical semantics, relying instead on state-transitional semantics enriched with hybrid automata semantics for the continuous states. This complex semantics makes analysis and comparisons to other action formalisms difficult. In this paper, we propose a natural extension of Reiter's situation calculus theories inspired by hybrid automata. The kinship between PDDL+ and hybrid automata allows us to develop a direct mapping between PDDL+ and situation calculus, thereby supplying PDDL+ with a logical semantics and the situation calculus with a modern way of representing autonomous processes. We outline the potential benefits of the mapping by suggesting a new approach to effective planning in PDDL+.
* arXiv admin note: text overlap with arXiv:1807.04861
Towards A Logical Account of Epistemic Causality
Oct 31, 2019
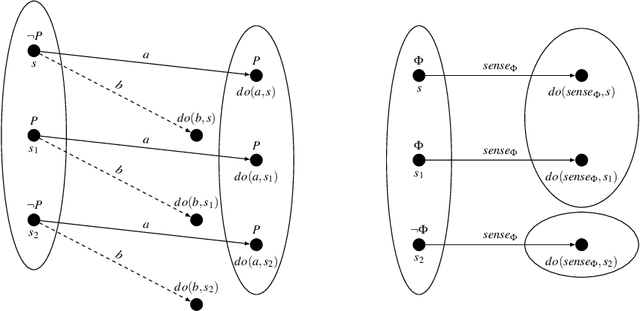

Abstract:Reasoning about observed effects and their causes is important in multi-agent contexts. While there has been much work on causality from an objective standpoint, causality from the point of view of some particular agent has received much less attention. In this paper, we address this issue by incorporating an epistemic dimension to an existing formal model of causality. We define what it means for an agent to know the causes of an effect. Then using a counterexample, we prove that epistemic causality is a different notion from its objective counterpart.
* In Proceedings CREST 2019, arXiv:1910.13641
Hybrid Temporal Situation Calculus
Jul 12, 2018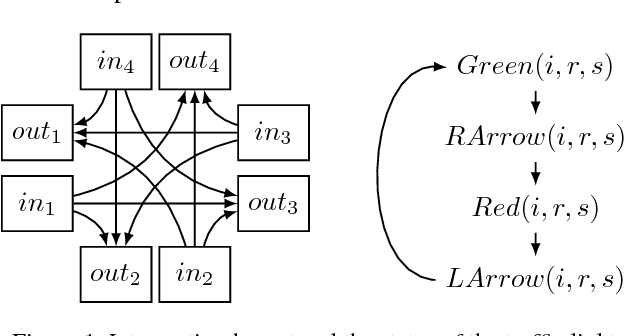
Abstract:The ability to model continuous change in Reiter's temporal situation calculus action theories has attracted a lot of interest. In this paper, we propose a new development of his approach, which is directly inspired by hybrid systems in control theory. Specifically, while keeping the foundations of Reiter's axiomatization, we propose an elegant extension of his approach by adding a time argument to all fluents that represent continuous change. Thereby, we insure that change can happen not only because of actions, but also due to the passage of time. We present a systematic methodology to derive, from simple premises, a new group of axioms which specify how continuous fluents change over time within a situation. We study regression for our new temporal basic action theories and demonstrate what reasoning problems can be solved. Finally, we formally show that our temporal basic action theories indeed capture hybrid automata.
Progression of Decomposed Local-Effect Action Theories
May 12, 2017Abstract:In many tasks related to reasoning about consequences of a logical theory, it is desirable to decompose the theory into a number of weakly-related or independent components. However, a theory may represent knowledge that is subject to change, as a result of executing actions that have effects on some of the initial properties mentioned in the theory. Having once computed a decomposition of a theory, it is advantageous to know whether a decomposition has to be computed again in the newly-changed theory (obtained from taking into account changes resulting from execution of an action). In the paper, we address this problem in the scope of the situation calculus, where a change of an initial theory is related to the notion of progression. Progression provides a form of forward reasoning; it relies on forgetting values of those properties, which are subject to change, and computing new values for them. We consider decomposability and inseparability, two component properties known from the literature, and contribute by 1) studying the conditions when these properties are preserved and 2) when they are lost wrt progression and the related operation of forgetting. To show the latter, we demonstrate the boundaries using a number of negative examples. To show the former, we identify cases when these properties are preserved under forgetting and progression of initial theories in local-effect basic action theories of the situation calculus. Our paper contributes to bridging two different communities in Knowledge Representation, namely research on modularity and research on reasoning about actions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge