Machine Learning with Probabilistic Law Discovery: A Concise Introduction

Probabilistic Law Discovery (PLD) is a logic based Machine Learning method, which implements a variant of probabilistic rule learning. In several aspects, PLD is close to Decision Tree/Random Forest methods, but it differs significantly in how relevant rules are defined. The learning procedure of PLD solves the optimization problem related to the search for rules (called probabilistic laws), which have a minimal length and relatively high probability. At inference, ensembles of these rules are used for prediction. Probabilistic laws are human-readable and PLD based models are transparent and inherently interpretable. Applications of PLD include classification/clusterization/regression tasks, as well as time series analysis/anomaly detection and adaptive (robotic) control. In this paper, we outline the main principles of PLD, highlight its benefits and limitations and provide some application guidelines.

Interpretable Reinforcement Learning with Multilevel Subgoal Discovery

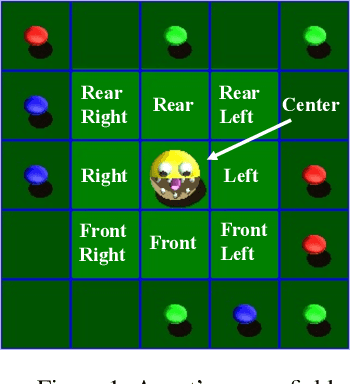
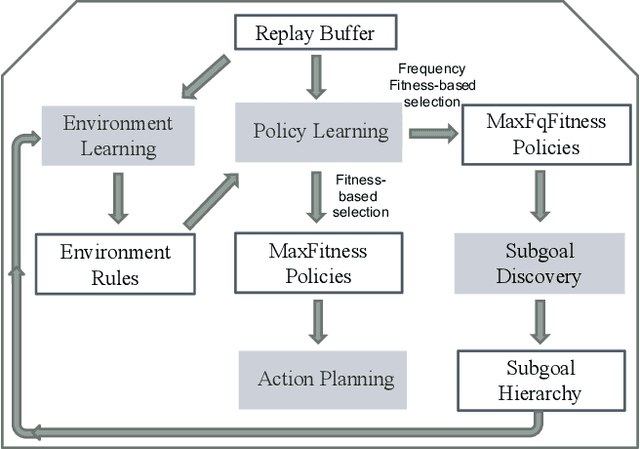
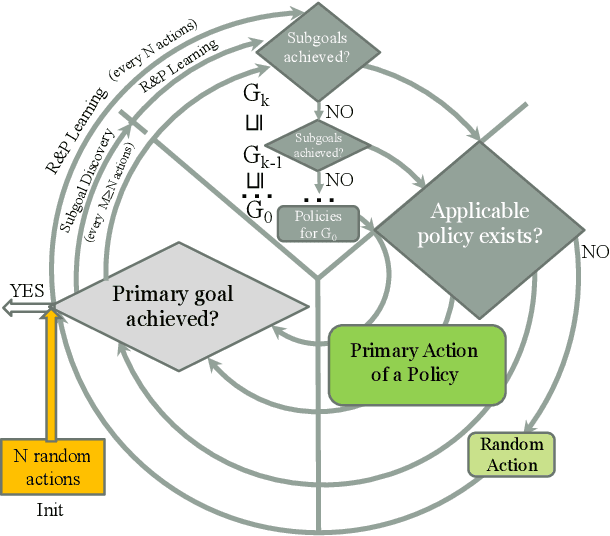
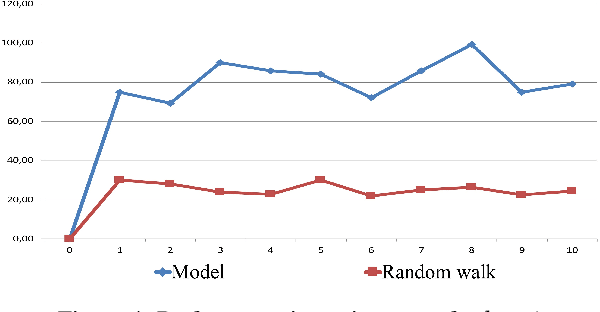
We propose a novel Reinforcement Learning model for discrete environments, which is inherently interpretable and supports the discovery of deep subgoal hierarchies. In the model, an agent learns information about environment in the form of probabilistic rules, while policies for (sub)goals are learned as combinations thereof. No reward function is required for learning; an agent only needs to be given a primary goal to achieve. Subgoals of a goal G from the hierarchy are computed as descriptions of states, which if previously achieved increase the total efficiency of the available policies for G. These state descriptions are introduced as new sensor predicates into the rule language of the agent, which allows for sensing important intermediate states and for updating environment rules and policies accordingly.

DeFind: A Protege Plugin for Computing Concept Definitions in EL Ontologies

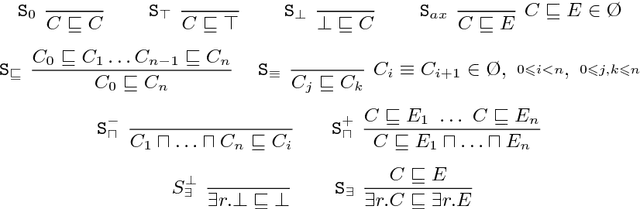
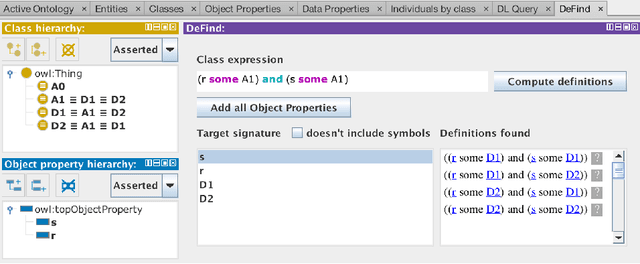
We introduce an extension to the Protege ontology editor, which allows for discovering concept definitions, which are not explicitly present in axioms, but are logically implied by an ontology. The plugin supports ontologies formulated in the Description Logic EL, which underpins the OWL 2 EL profile of the Web Ontology Language and despite its limited expressiveness captures most of the biomedical ontologies published on the Web. The developed tool allows to verify whether a concept can be defined using a vocabulary of interest specified by a user. In particular, it allows to decide whether some vocabulary items can be omitted in a formulation of a complex concept. The corresponding definitions are presented to the user and are provided with explanations generated by an ontology reasoner.

On the Complexity of Semantic Integration of OWL Ontologies

We propose a new mechanism for integration of OWL ontologies using semantic import relations. In contrast to the standard OWL importing, we do not require all axioms of the imported ontologies to be taken into account for reasoning tasks, but only their logical implications over a chosen signature. This property comes natural in many ontology integration scenarios, especially when the number of ontologies is large. In this paper, we study the complexity of reasoning over ontologies with semantic import relations and establish a range of tight complexity bounds for various fragments of OWL.

Progression of Decomposed Local-Effect Action Theories

In many tasks related to reasoning about consequences of a logical theory, it is desirable to decompose the theory into a number of weakly-related or independent components. However, a theory may represent knowledge that is subject to change, as a result of executing actions that have effects on some of the initial properties mentioned in the theory. Having once computed a decomposition of a theory, it is advantageous to know whether a decomposition has to be computed again in the newly-changed theory (obtained from taking into account changes resulting from execution of an action). In the paper, we address this problem in the scope of the situation calculus, where a change of an initial theory is related to the notion of progression. Progression provides a form of forward reasoning; it relies on forgetting values of those properties, which are subject to change, and computing new values for them. We consider decomposability and inseparability, two component properties known from the literature, and contribute by 1) studying the conditions when these properties are preserved and 2) when they are lost wrt progression and the related operation of forgetting. To show the latter, we demonstrate the boundaries using a number of negative examples. To show the former, we identify cases when these properties are preserved under forgetting and progression of initial theories in local-effect basic action theories of the situation calculus. Our paper contributes to bridging two different communities in Knowledge Representation, namely research on modularity and research on reasoning about actions.