Training-Free Query Optimization via LLM-Based Plan Similarity

Large language model (LLM) embeddings offer a promising new avenue for database query optimization. In this paper, we explore how pre-trained execution plan embeddings can guide SQL query execution without the need for additional model training. We introduce LLM-PM (LLM-based Plan Mapping), a framework that embeds the default execution plan of a query, finds its k nearest neighbors among previously executed plans, and recommends database hintsets based on neighborhood voting. A lightweight consistency check validates the selected hint, while a fallback mechanism searches the full hint space when needed. Evaluated on the JOB-CEB benchmark using OpenGauss, LLM-PM achieves an average speed-up of 21% query latency reduction. This work highlights the potential of LLM-powered embeddings to deliver practical improvements in query performance and opens new directions for training-free, embedding-based optimizer guidance systems.

Machine Learning with Probabilistic Law Discovery: A Concise Introduction

Probabilistic Law Discovery (PLD) is a logic based Machine Learning method, which implements a variant of probabilistic rule learning. In several aspects, PLD is close to Decision Tree/Random Forest methods, but it differs significantly in how relevant rules are defined. The learning procedure of PLD solves the optimization problem related to the search for rules (called probabilistic laws), which have a minimal length and relatively high probability. At inference, ensembles of these rules are used for prediction. Probabilistic laws are human-readable and PLD based models are transparent and inherently interpretable. Applications of PLD include classification/clusterization/regression tasks, as well as time series analysis/anomaly detection and adaptive (robotic) control. In this paper, we outline the main principles of PLD, highlight its benefits and limitations and provide some application guidelines.

Interpretable Reinforcement Learning with Multilevel Subgoal Discovery

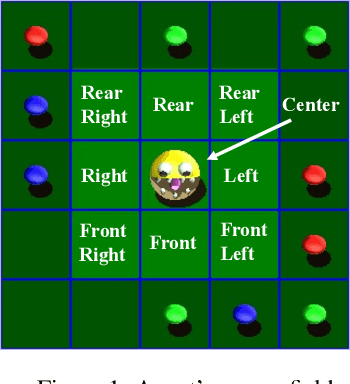
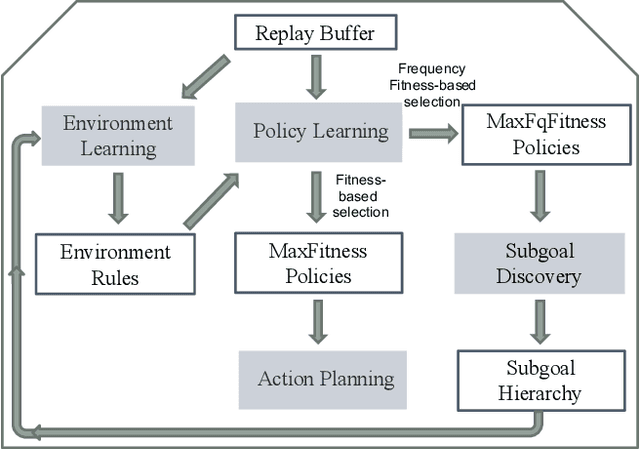
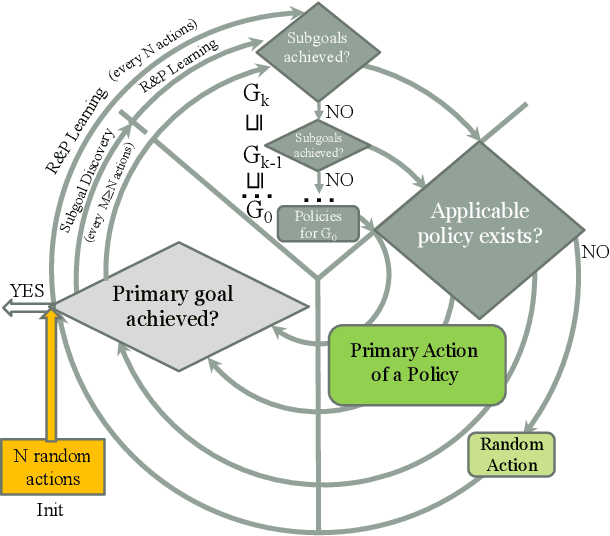
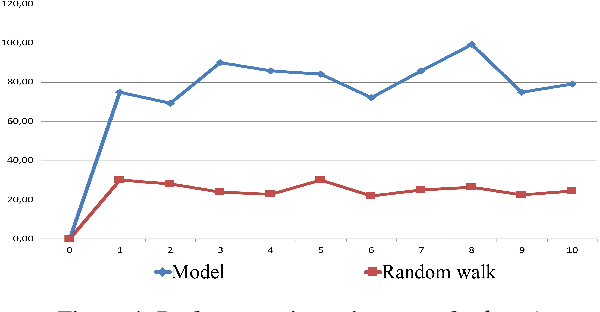
We propose a novel Reinforcement Learning model for discrete environments, which is inherently interpretable and supports the discovery of deep subgoal hierarchies. In the model, an agent learns information about environment in the form of probabilistic rules, while policies for (sub)goals are learned as combinations thereof. No reward function is required for learning; an agent only needs to be given a primary goal to achieve. Subgoals of a goal G from the hierarchy are computed as descriptions of states, which if previously achieved increase the total efficiency of the available policies for G. These state descriptions are introduced as new sensor predicates into the rule language of the agent, which allows for sensing important intermediate states and for updating environment rules and policies accordingly.