3D Shapes Local Geometry Codes Learning with SDF

A signed distance function (SDF) as the 3D shape description is one of the most effective approaches to represent 3D geometry for rendering and reconstruction. Our work is inspired by the state-of-the-art method DeepSDF that learns and analyzes the 3D shape as the iso-surface of its shell and this method has shown promising results especially in the 3D shape reconstruction and compression domain. In this paper, we consider the degeneration problem of reconstruction coming from the capacity decrease of the DeepSDF model, which approximates the SDF with a neural network and a single latent code. We propose Local Geometry Code Learning (LGCL), a model that improves the original DeepSDF results by learning from a local shape geometry of the full 3D shape. We add an extra graph neural network to split the single transmittable latent code into a set of local latent codes distributed on the 3D shape. Mentioned latent codes are used to approximate the SDF in their local regions, which will alleviate the complexity of the approximation compared to the original DeepSDF. Furthermore, we introduce a new geometric loss function to facilitate the training of these local latent codes. Note that other local shape adjusting methods use the 3D voxel representation, which in turn is a problem highly difficult to solve or even is insolvable. In contrast, our architecture is based on graph processing implicitly and performs the learning regression process directly in the latent code space, thus make the proposed architecture more flexible and also simple for realization. Our experiments on 3D shape reconstruction demonstrate that our LGCL method can keep more details with a significantly smaller size of the SDF decoder and outperforms considerably the original DeepSDF method under the most important quantitative metrics.

Slimmable Compressive Autoencoders for Practical Neural Image Compression

Neural image compression leverages deep neural networks to outperform traditional image codecs in rate-distortion performance. However, the resulting models are also heavy, computationally demanding and generally optimized for a single rate, limiting their practical use. Focusing on practical image compression, we propose slimmable compressive autoencoders (SlimCAEs), where rate (R) and distortion (D) are jointly optimized for different capacities. Once trained, encoders and decoders can be executed at different capacities, leading to different rates and complexities. We show that a successful implementation of SlimCAEs requires suitable capacity-specific RD tradeoffs. Our experiments show that SlimCAEs are highly flexible models that provide excellent rate-distortion performance, variable rate, and dynamic adjustment of memory, computational cost and latency, thus addressing the main requirements of practical image compression.

Sparse data interpolation using the geodesic distance affinity space

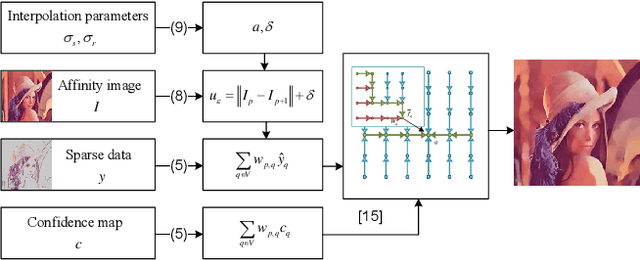
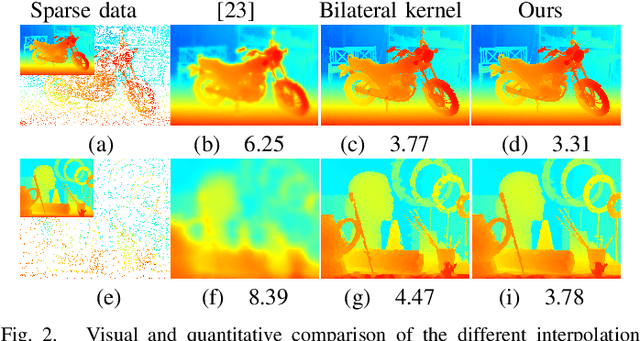
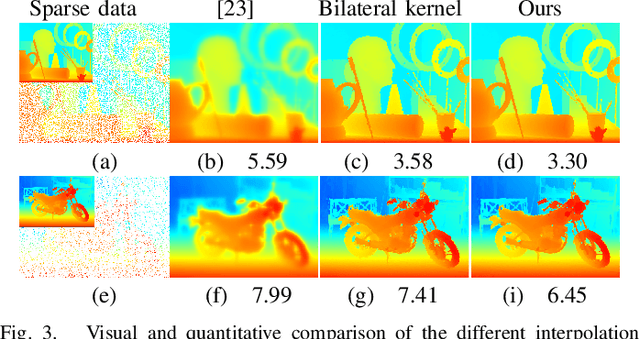
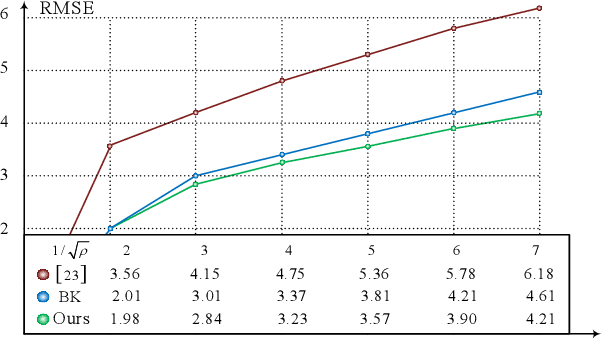
In this paper, we adapt the geodesic distance-based recursive filter to the sparse data interpolation problem. The proposed technique is general and can be easily applied to any kind of sparse data. We demonstrate the superiority over other interpolation techniques in three experiments for qualitative and quantitative evaluation. In addition, we compare our method with the popular interpolation algorithm presented in the EpicFlow optical flow paper that is intuitively motivated by a similar geodesic distance principle. The comparison shows that our algorithm is more accurate and considerably faster than the EpicFlow interpolation technique.

One-view occlusion detection for stereo matching with a fully connected CRF model

In this paper, we extend the standard belief propagation (BP) sequential technique proposed in the tree-reweighted sequential method to the fully connected CRF models with the geodesic distance affinity. The proposed method has been applied to the stereo matching problem. Also a new approach to the BP marginal solution is proposed that we call one-view occlusion detection (OVOD). In contrast to the standard winner takes all (WTA) estimation, the proposed OVOD solution allows to find occluded regions in the disparity map and simultaneously improve the matching result. As a result we can perform only one energy minimization process and avoid the cost calculation for the second view and the left-right check procedure. We show that the OVOD approach considerably improves results for cost augmentation and energy minimization techniques in comparison with the standard one-view affinity space implementation. We apply our method to the Middlebury data set and reach state-of-the-art especially for median, average and mean squared error metrics.

Extended Dynamic Programming and Fast Multidimensional Search Algorithm for Energy Minization in Stereo and Motion

This paper presents a novel extended dynamic programming approach for energy minimization (EDP) to solve the correspondence problem for stereo and motion. A significant speedup is achieved using a recursive minimum search strategy (RMS). The mentioned speedup is particularly important if the disparity space is 2D as well as 3D. The proposed RMS can also be applied in the well-known dynamic programming (DP) approach for stereo and motion. In this case, the general 2D problem of the global discrete energy minimization is reduced to several mutually independent sub-problems of the one-dimensional minimization. The EDP method is used when the approximation of the general 2D discrete energy minimization problem is considered. Then the RMS algorithm is an essential part of the EDP method. Using the EDP algorithm we obtain a lower energy bound than the graph cuts (GC) expansion technique on stereo and motion problems. The proposed calculation scheme possesses natural parallelism and can be realized on graphics processing unit (GPU) platforms, and can be potentially restricted further by the number of scanlines in the image plane. Furthermore, the RMS and EDP methods can be used in any optimization problem where the objective function meets specific conditions in the smoothness term.