Michela Azzarito
Model-based multi-parameter mapping
Feb 02, 2021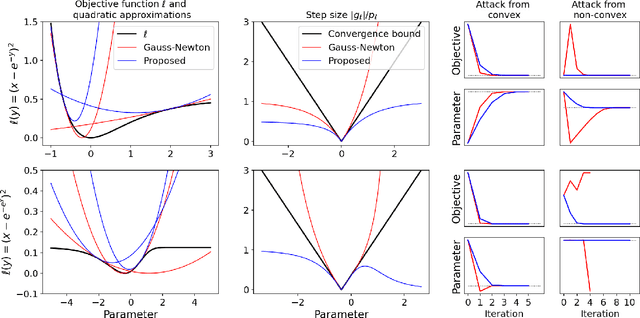
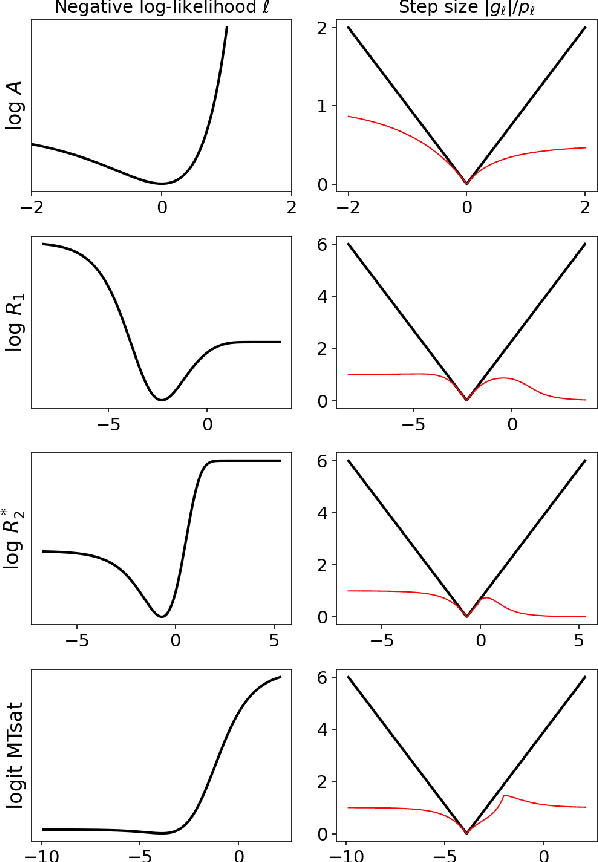
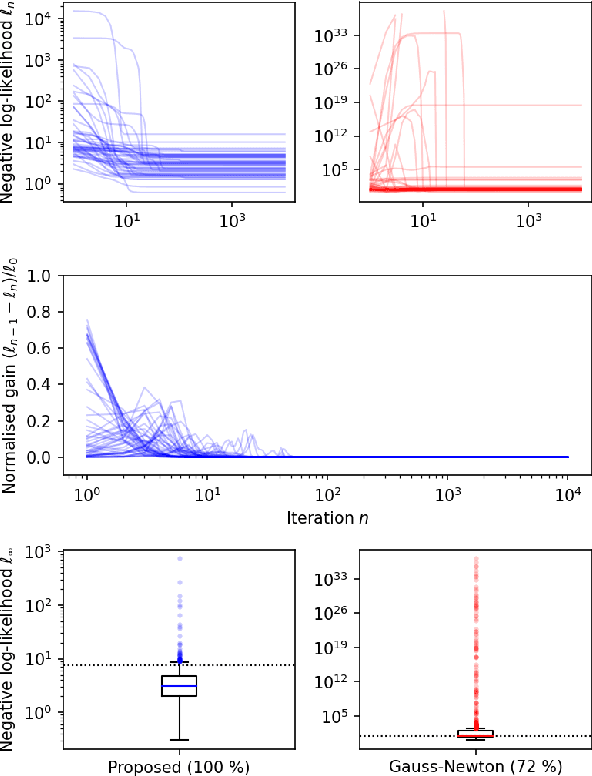
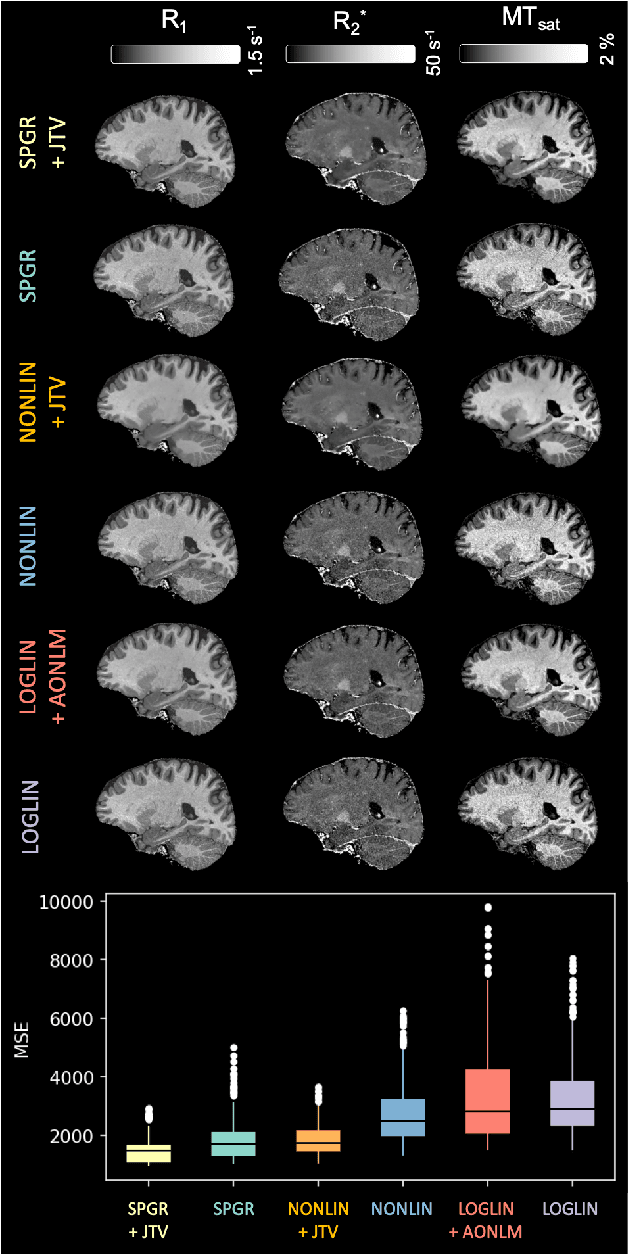
Abstract:Quantitative MR imaging is increasingly favoured for its richer information content and standardised measures. However, extracting quantitative parameters such as the longitudinal relaxation rate (R1), apparent transverse relaxation rate (R2*), or magnetisation-transfer saturation (MTsat) involves inverting a highly non-linear function. Estimations often assume noise-free measurements and use subsets of the data to solve for different quantities in isolation, with error propagating through each computation. Instead, a probabilistic generative model of the entire dataset can be formulated and inverted to jointly recover parameter estimates with a well-defined probabilistic meaning (e.g., maximum likelihood or maximum a posteriori). In practice, iterative methods must be used but convergence is difficult due to the non-convexity of the log-likelihood; yet, we show that it can be achieved thanks to a novel approximate Hessian and, with it, reliable parameter estimates obtained. Here, we demonstrate the utility of this flexible framework in the context of the popular multi-parameter mapping framework and further show how to incorporate a denoising prior and predict posterior uncertainty. Our implementation uses a PyTorch backend and benefits from GPU acceleration. It is available at https://github.com/balbasty/nitorch.
Joint Total Variation ESTATICS for Robust Multi-Parameter Mapping
May 28, 2020


Abstract:Quantitative magnetic resonance imaging (qMRI) derives tissue-specific parameters -- such as the apparent transverse relaxation rate R2*, the longitudinal relaxation rate R1 and the magnetisation transfer saturation -- that can be compared across sites and scanners and carry important information about the underlying microstructure. The multi-parameter mapping (MPM) protocol takes advantage of multi-echo acquisitions with variable flip angles to extract these parameters in a clinically acceptable scan time. In this context, ESTATICS performs a joint loglinear fit of multiple echo series to extract R2* and multiple extrapolated intercepts, thereby improving robustness to motion and decreasing the variance of the estimators. In this paper, we extend this model in two ways: (1) by introducing a joint total variation (JTV) prior on the intercepts and decay, and (2) by deriving a nonlinear maximum \emph{a posteriori} estimate. We evaluated the proposed algorithm by predicting left-out echoes in a rich single-subject dataset. In this validation, we outperformed other state-of-the-art methods and additionally showed that the proposed approach greatly reduces the variance of the estimated maps, without introducing bias.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge