FNetAR: Mixing Tokens with Autoregressive Fourier Transforms

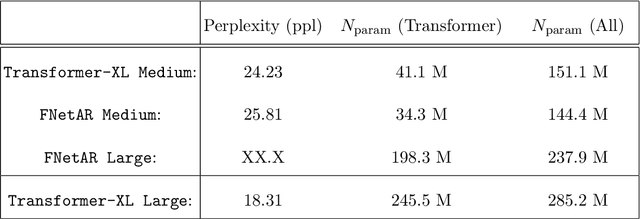
In this note we examine the autoregressive generalization of the FNet algorithm, in which self-attention layers from the standard Transformer architecture are substituted with a trivial sparse-uniformsampling procedure based on Fourier transforms. Using the Wikitext-103 benchmark, we demonstratethat FNetAR retains state-of-the-art performance (25.8 ppl) on the task of causal language modelingcompared to a Transformer-XL baseline (24.2 ppl) with only half the number self-attention layers,thus providing further evidence for the superfluity of deep neural networks with heavily compoundedattention mechanisms. The autoregressive Fourier transform could likely be used for parameterreduction on most Transformer-based time-series prediction models.

SyDeBO: Symbolic-Decision-Embedded Bilevel Optimization for Long-Horizon Manipulation in Dynamic Environments

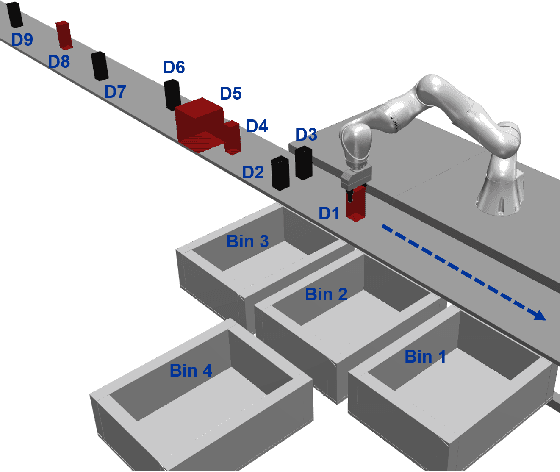
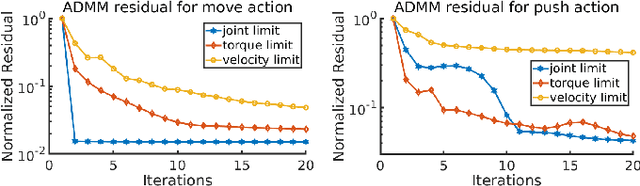
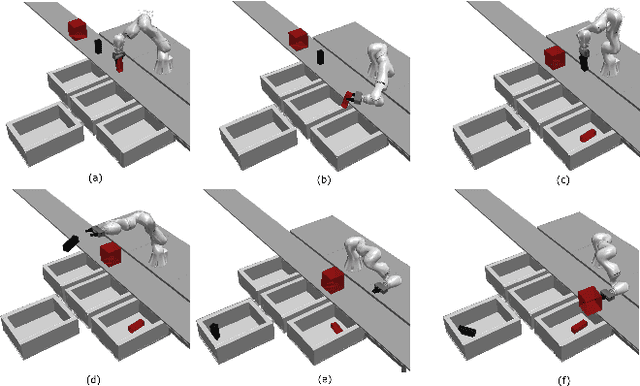
This study proposes a Task and Motion Planning (TAMP) method with symbolic decisions embedded in a bilevel optimization. This TAMP method exploits the discrete structure of sequential manipulation for long-horizon and versatile tasks in dynamically changing environments. At the symbolic planning level, we propose a scalable decision-making method for long-horizon manipulation tasks using the Planning Domain Definition Language (PDDL) with causal graph decomposition. At the motion planning level, we devise a trajectory optimization (TO) approach based on the Alternating Direction Method of Multipliers (ADMM), suitable for solving constrained, large-scale nonlinear optimization in a distributed manner. Distinct from conventional geometric motion planners, our approach generates highly dynamic manipulation motions by incorporating the full robot and object dynamics. Furthermore, in lieu of a hierarchical planning approach, we solve a holistically integrated bilevel optimization problem involving costs from both the low-level TO and the high-level search. Simulation and experimental results demonstrate dynamic manipulation for long-horizon object sorting tasks in clutter and on a moving conveyor belt.

Moment-Matching Graph-Networks for Causal Inference

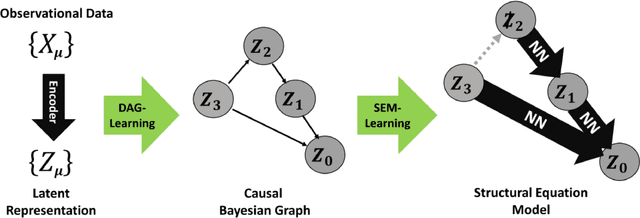
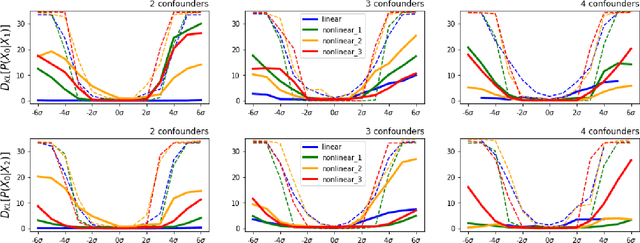
In this note we explore a fully unsupervised deep-learning framework for simulating non-linear structural equation models from observational training data. The main contribution of this note is an architecture for applying moment-matching loss functions to the edges of a causal Bayesian graph, resulting in a generative conditional-moment-matching graph-neural-network. This framework thus enables automated sampling of latent space conditional probability distributions for various graphical interventions, and is capable of generating out-of-sample interventional probabilities that are often faithful to the ground truth distributions well beyond the range contained in the training set. These methods could in principle be used in conjunction with any existing autoencoder that produces a latent space representation containing causal graph structures.