Unsupervised Identification and Removal of Spurious Correlations During Fine-Tuning

Fine-tuning a pretrained language model on a curated dataset can produce spurious correlations between the fine-tuning task and unintended latent factors -- such as misaligned personas or political slant -- that the curation procedure has entangled with the task. The model can latch onto these spurious correlations, leading to bias and reduced out-of-distribution generalisation. We prove that under reasonable assumptions on task complexity and the spurious correlation, such latent factors can be identified, without supervision, from the weights of a naive LoRA fine-tune. Existing approaches to removing bias, such as activation steering, remove identified factors from residual-stream activations, either at inference or during training. We argue, however, that the goal should be to remove the spurious correlation, not the latent factor itself, as the pretrained model may rely on it for genuine task signal. To enable this, we propose GRASP, GRadient projection of Associated Spurious Patterns, which prevents the model from acquiring new reliance on the identified latent factor while preserving any pretrained content along it. We validate on three fine-tuning tasks. The first two involve emergent misalignment, where fine-tuning on a narrow task -- in our case, writing insecure code and giving bad medical advice -- leads to misaligned responses on unrelated topics. Here our method completely removes misalignment in the insecure code case and reduces them by ~5x in the bad medical advice case, beating all baselines in the trade-off between misalignment-reduction and task-preservation. The last is a novel political-bias experiment, where fine-tuning on right-skewed Reddit financial-advice data causes political-lean drift on unrelated topics. Here our method reduces drift by more than half, while improving financial task performance, beating all baselines.

Causal Representation Learning for Generalisable Recommendation

Predictive models trained on observational data often fail to generalise to the distributions they encounter when deployed, especially when the training data is a product of the system being optimised. Recommender systems are a canonical example: they are trained on interaction logs confounded by the deployed policy, past user behaviour, and platform filtering. As a result, the training distribution differs substantially from the candidate distribution scored at serving time, a gap that makes offline metrics unreliable predictors of online performance. We address the distribution shift problem with a method motivated by causal representation learning (CRL). We propose an information-theoretic disentanglement criterion and prove that its optimum depends only on the causal components of the input. We then derive a tractable variational lower bound that makes the criterion optimisable from finite observational data alone. The scope of our method is narrower than that of much of the CRL literature, in that we target better generalisation under distribution shift, not full identification of all latent causal factors. This narrower target is what makes the method practical, requiring only the existing confounded logs, applying to any standard supervised model, and adding no inference-time cost. Our headline evaluation is an A/B test with millions of users on Spotify, applied to a production ranker for personalised playlist generation. A capacity-matched CRL variant performed on par offline but delivered substantial online gains in listener engagement. Complementary evidence on the public KuaiRand recommendation dataset and a synthetic benchmark with known causal structure shows the same pattern: offline parity with baseline, gains under distribution shift. Across all three settings, adding our causal disentanglement objective yields meaningfully better out-of-distribution generalisation.

Local Interference: Removing Interference Bias in Semi-Parametric Causal Models

Interference bias is a major impediment to identifying causal effects in real-world settings. For example, vaccination reduces the transmission of a virus in a population such that everyone benefits -- even those who are not treated. This is a source of bias that must be accounted for if one wants to learn the true effect of a vaccine on an individual's immune system. Previous approaches addressing interference bias require strong domain knowledge in the form of a graphical interaction network fully describing interference between units. Moreover, they place additional constraints on the form the interference can take, such as restricting to linear outcome models, and assuming that interference experienced by a unit does not depend on the unit's covariates. Our work addresses these shortcomings. We first provide and justify a novel definition of causal models with local interference. We prove that the True Average Causal Effect, a measure of causality where interference has been removed, can be identified in certain semi-parametric models satisfying this definition. These models allow for non-linearity, and also for interference to depend on a unit's covariates. An analytic estimand for the True Average Causal Effect is given in such settings. We further prove that the True Average Causal Effect cannot be identified in arbitrary models with local interference, showing that identification requires semi-parametric assumptions. Finally, we provide an empirical validation of our method on both simulated and real-world datasets.

The Hardness of Validating Observational Studies with Experimental Data

Observational data is often readily available in large quantities, but can lead to biased causal effect estimates due to the presence of unobserved confounding. Recent works attempt to remove this bias by supplementing observational data with experimental data, which, when available, is typically on a smaller scale due to the time and cost involved in running a randomised controlled trial. In this work, we prove a theorem that places fundamental limits on this ``best of both worlds'' approach. Using the framework of impossible inference, we show that although it is possible to use experimental data to \emph{falsify} causal effect estimates from observational data, in general it is not possible to \emph{validate} such estimates. Our theorem proves that while experimental data can be used to detect bias in observational studies, without additional assumptions on the smoothness of the correction function, it can not be used to remove it. We provide a practical example of such an assumption, developing a novel Gaussian Process based approach to construct intervals which contain the true treatment effect with high probability, both inside and outside of the support of the experimental data. We demonstrate our methodology on both simulated and semi-synthetic datasets and make the \href{https://github.com/Jakefawkes/Obs_and_exp_data}{code available}.

Contrastive representations of high-dimensional, structured treatments

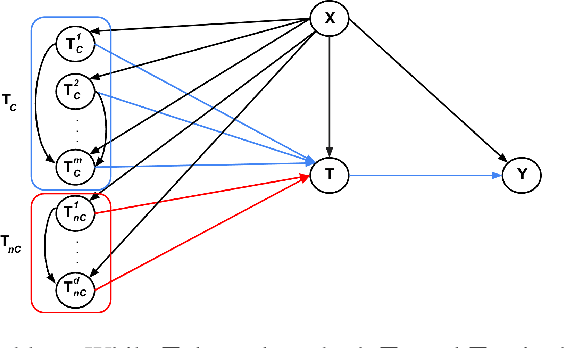
Estimating causal effects is vital for decision making. In standard causal effect estimation, treatments are usually binary- or continuous-valued. However, in many important real-world settings, treatments can be structured, high-dimensional objects, such as text, video, or audio. This provides a challenge to traditional causal effect estimation. While leveraging the shared structure across different treatments can help generalize to unseen treatments at test time, we show in this paper that using such structure blindly can lead to biased causal effect estimation. We address this challenge by devising a novel contrastive approach to learn a representation of the high-dimensional treatments, and prove that it identifies underlying causal factors and discards non-causally relevant factors. We prove that this treatment representation leads to unbiased estimates of the causal effect, and empirically validate and benchmark our results on synthetic and real-world datasets.

Spillover Detection for Donor Selection in Synthetic Control Models

Synthetic control (SC) models are widely used to estimate causal effects in settings with observational time-series data. To identify the causal effect on a target unit, SC requires the existence of correlated units that are not impacted by the intervention. Given one of these potential donor units, how can we decide whether it is in fact a valid donor - that is, one not subject to spillover effects from the intervention? Such a decision typically requires appealing to strong a priori domain knowledge specifying the units, which becomes infeasible in situations with large pools of potential donors. In this paper, we introduce a practical, theoretically-grounded donor selection procedure, aiming to weaken this domain knowledge requirement. Our main result is a Theorem that yields the assumptions required to identify donor values at post-intervention time points using only pre-intervention data. We show how this Theorem - and the assumptions underpinning it - can be turned into a practical method for detecting potential spillover effects and excluding invalid donors when constructing SCs. Importantly, we employ sensitivity analysis to formally bound the bias in our SC causal estimate in situations where an excluded donor was indeed valid, or where a selected donor was invalid. Using ideas from the proximal causal inference and instrumental variables literature, we show that the excluded donors can nevertheless be leveraged to further debias causal effect estimates. Finally, we illustrate our donor selection procedure on both simulated and real-world datasets.