Latent Representation Prediction Networks

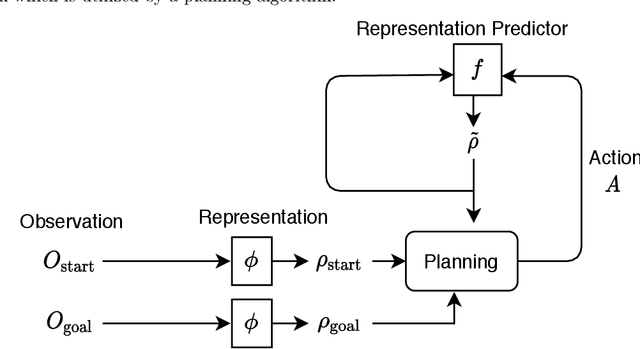
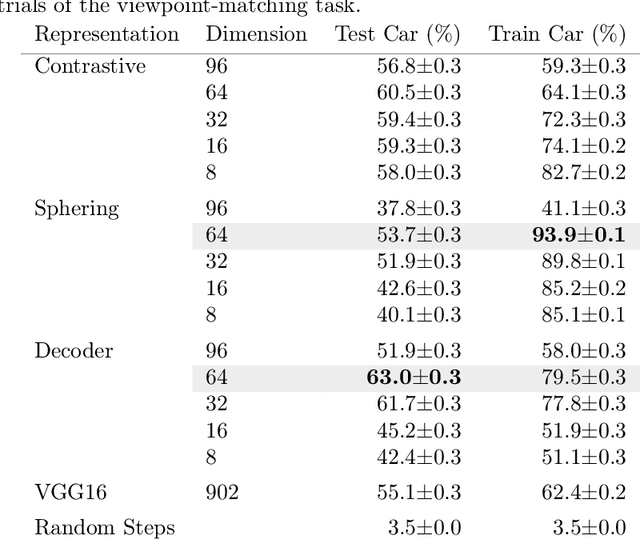
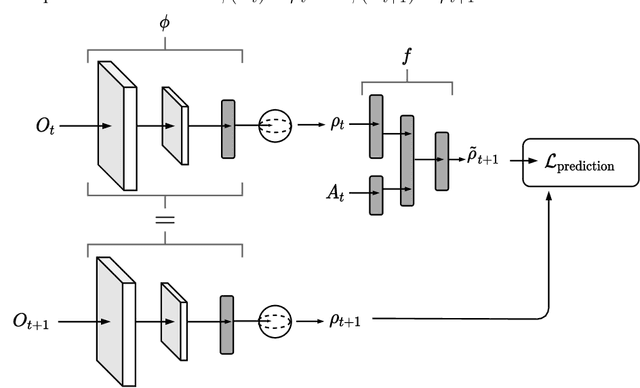
Deeply-learned planning methods are often based on learning representations that are optimized for unrelated tasks. For example, they might be trained on reconstructing the environment. These representations are then combined with predictor functions for simulating rollouts to navigate the environment. We find this principle of learning representations unsatisfying and propose to learn them such that they are directly optimized for the task at hand: to be maximally predictable for the predictor function. This results in representations that are by design optimal for the downstream task of planning, where the learned predictor function is used as a forward model. To this end, we propose a new way of jointly learning this representation along with the prediction function, a system we dub Latent Representation Prediction Network (LARP). The prediction function is used as a forward model for search on a graph in a viewpoint-matching task and the representation learned to maximize predictability is found to outperform a pre-trained representation. Our approach is shown to be more sample-efficient than standard reinforcement learning methods and our learned representation transfers successfully to dissimilar objects.

Gradient-based Training of Slow Feature Analysis by Differentiable Approximate Whitening

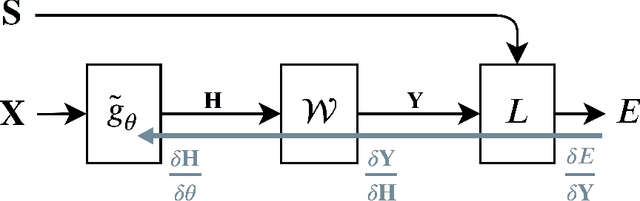
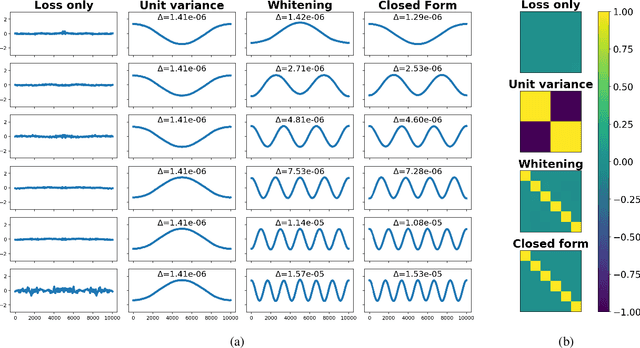
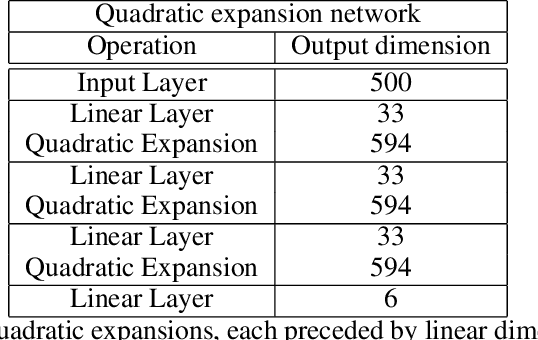
This paper proposes Power Slow Feature Analysis, a gradient-based method to extract temporally-slow features from a high-dimensional input stream that varies on a faster time-scale, and a variant of Slow Feature Analysis (SFA). While displaying performance comparable to hierarchical extensions to the SFA algorithm, such as Hierarchical Slow Feature Analysis, for a small number of output-features, our algorithm allows end-to-end training of arbitrary differentiable approximators (e.g., deep neural networks). We provide experimental evidence that PowerSFA is able to extract meaningful and informative low-dimensional features in the case of a) synthetic low-dimensional data, b) visual data, and also for c) a general dataset for which symmetric non-temporal relations between points can be defined.

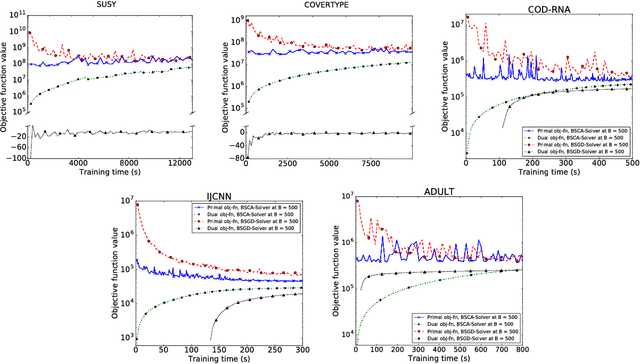
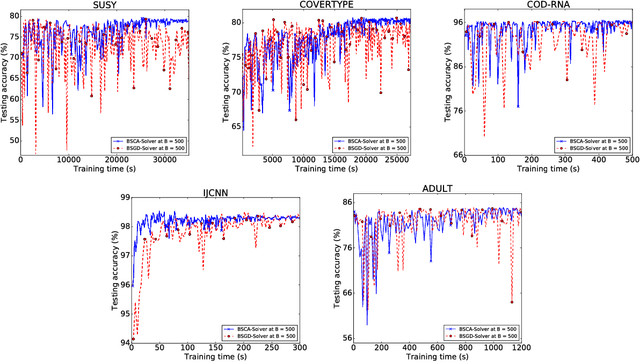
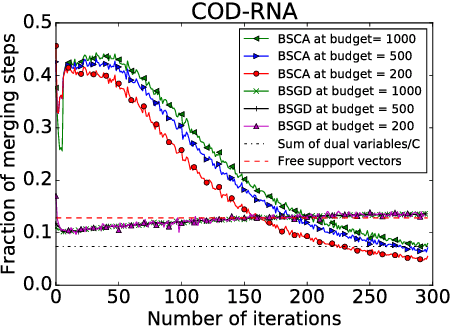
Dual SVM Training on a Budget

We present a dual subspace ascent algorithm for support vector machine training that respects a budget constraint limiting the number of support vectors. Budget methods are effective for reducing the training time of kernel SVM while retaining high accuracy. To date, budget training is available only for primal (SGD-based) solvers. Dual subspace ascent methods like sequential minimal optimization are attractive for their good adaptation to the problem structure, their fast convergence rate, and their practical speed. By incorporating a budget constraint into a dual algorithm, our method enjoys the best of both worlds. We demonstrate considerable speed-ups over primal budget training methods.