Sahar Qaadan
Dual SVM Training on a Budget
Jun 26, 2018
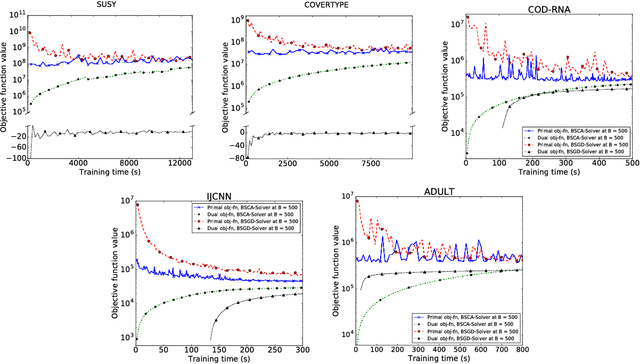
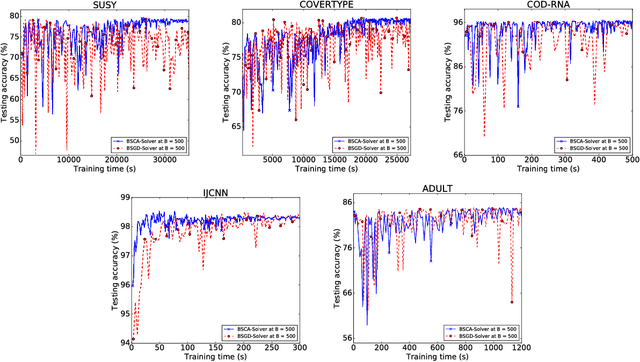
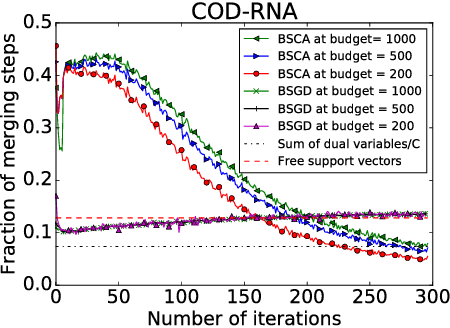
Abstract:We present a dual subspace ascent algorithm for support vector machine training that respects a budget constraint limiting the number of support vectors. Budget methods are effective for reducing the training time of kernel SVM while retaining high accuracy. To date, budget training is available only for primal (SGD-based) solvers. Dual subspace ascent methods like sequential minimal optimization are attractive for their good adaptation to the problem structure, their fast convergence rate, and their practical speed. By incorporating a budget constraint into a dual algorithm, our method enjoys the best of both worlds. We demonstrate considerable speed-ups over primal budget training methods.
Speeding Up Budgeted Stochastic Gradient Descent SVM Training with Precomputed Golden Section Search
Jun 26, 2018



Abstract:Limiting the model size of a kernel support vector machine to a pre-defined budget is a well-established technique that allows to scale SVM learning and prediction to large-scale data. Its core addition to simple stochastic gradient training is budget maintenance through merging of support vectors. This requires solving an inner optimization problem with an iterative method many times per gradient step. In this paper we replace the iterative procedure with a fast lookup. We manage to reduce the merging time by up to 65% and the total training time by 44% without any loss of accuracy.
Multi-Merge Budget Maintenance for Stochastic Gradient Descent SVM Training
Jun 26, 2018



Abstract:Budgeted Stochastic Gradient Descent (BSGD) is a state-of-the-art technique for training large-scale kernelized support vector machines. The budget constraint is maintained incrementally by merging two points whenever the pre-defined budget is exceeded. The process of finding suitable merge partners is costly; it can account for up to 45% of the total training time. In this paper we investigate computationally more efficient schemes that merge more than two points at once. We obtain significant speed-ups without sacrificing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge