Mercedes Garcia-Salguero
Fast and Robust Certifiable Estimation of the Relative Pose Between Two Calibrated Cameras
Jan 21, 2021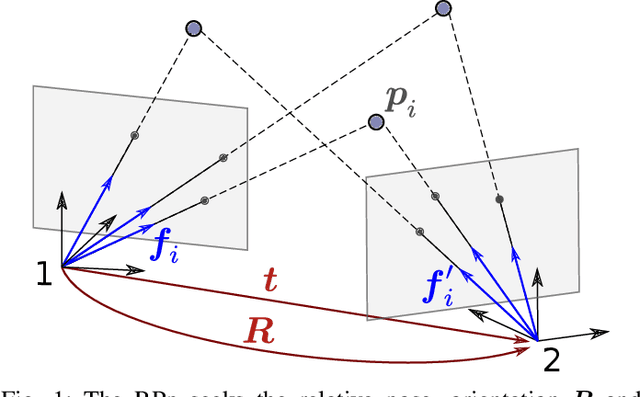
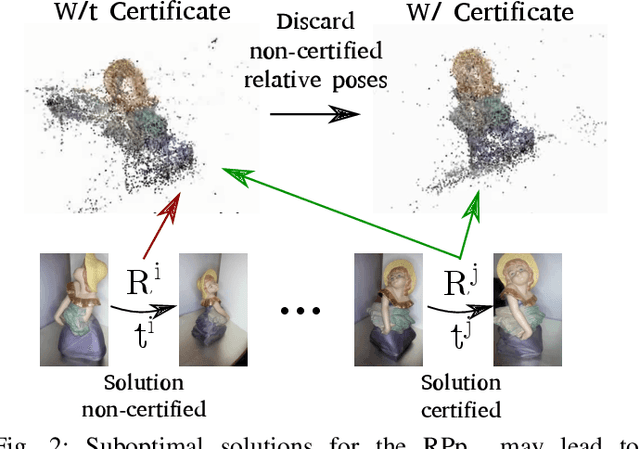
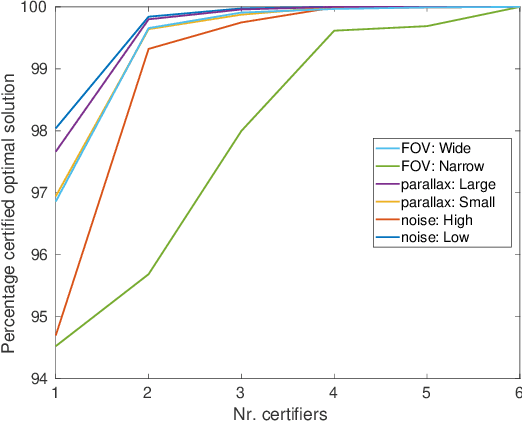
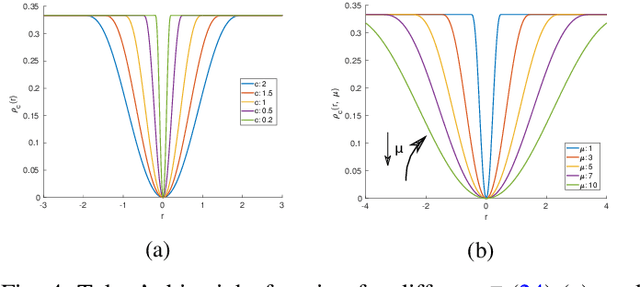
Abstract:The Relative Pose problem (RPp) for cameras aims to estimate the relative orientation and translation (pose) given a set of pair-wise feature correspondences between two central and calibrated cameras. The RPp is stated as an optimization problem where the squared, normalized epipolar error is minimized over the set of normalized essential matrices. In this work, we contribute an efficient and complete algorithm based on results from duality theory that is able to certify whether the solution to a RPp instance is the global optimum. Specifically, we present a family of certifiers that is shown to increase the ratio of detected optimal solutions. This set of certifiers is incorporated into an efficient essential matrix estimation pipeline that, given any initial guess for the RPp, refines it iteratively on the product space of 3D rotations and 2-sphere and thereupon, certifies the optimality of the solution. We integrate our fast certifiable pipeline into a robust framework that combines Graduated Non-convexity and the Black-Rangarajan duality between robust functions and line processes. This combination has been shown in the literature to outperform the robustness to outliers provided by approaches based on RANSAC. We proved through extensive experiments on synthetic and real data that the proposed framework provides a fast and robust relative pose estimation. We compare our proposal against the state-of-the-art methods on both accuracy and computational cost, and show that our estimations improve the output of the gold-standard approach for the RPp, the 2-view Bundle-Adjustment. We make the code publicly available \url{https://github.com/mergarsal/FastCertRelPose.git}.
Certifiable Relative Pose Estimation
Mar 30, 2020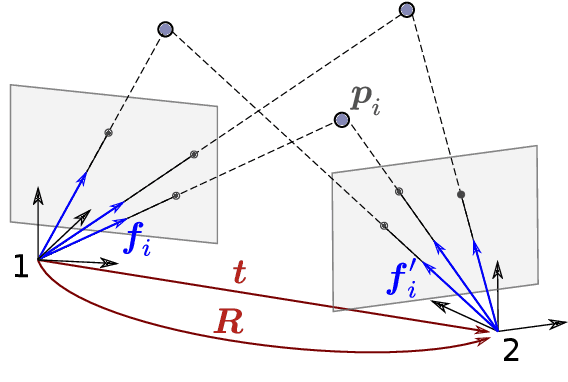

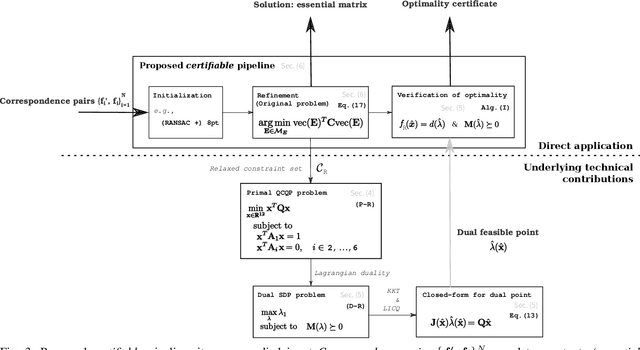
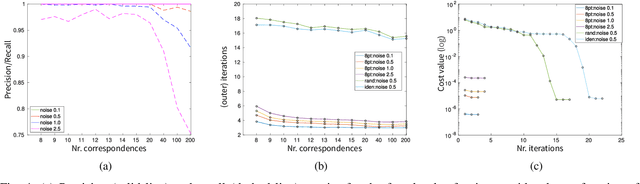
Abstract:In this paper we present the first fast optimality certifier for the non-minimal version of the Relative Pose problem for calibrated cameras from epipolar constraints. The proposed certifier is based on Lagrangian duality and relies on a novel closed-form expression for dual points. We also leverage an efficient solver that performs local optimization on the manifold of the original problem's non-convex domain. The optimality of the solution is then checked via our novel fast certifier. The extensive conducted experiments demonstrate that, despite its simplicity, this certifiable solver performs excellently on synthetic data, repeatedly attaining the (certified \textit{a posteriori}) optimal solution and shows a satisfactory performance on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge