Certifiable Relative Pose Estimation
Paper and Code
Mar 30, 2020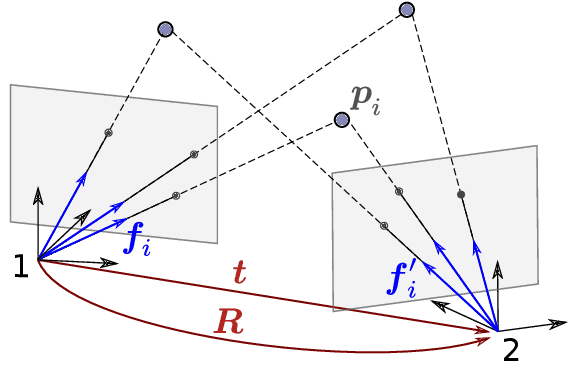

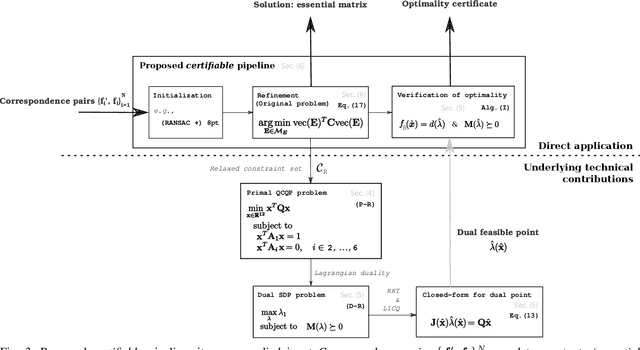
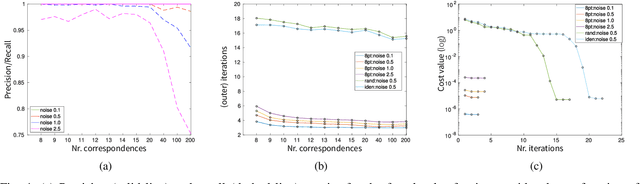
In this paper we present the first fast optimality certifier for the non-minimal version of the Relative Pose problem for calibrated cameras from epipolar constraints. The proposed certifier is based on Lagrangian duality and relies on a novel closed-form expression for dual points. We also leverage an efficient solver that performs local optimization on the manifold of the original problem's non-convex domain. The optimality of the solution is then checked via our novel fast certifier. The extensive conducted experiments demonstrate that, despite its simplicity, this certifiable solver performs excellently on synthetic data, repeatedly attaining the (certified \textit{a posteriori}) optimal solution and shows a satisfactory performance on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge