Non-Progressive Influence Maximization in Dynamic Social Networks

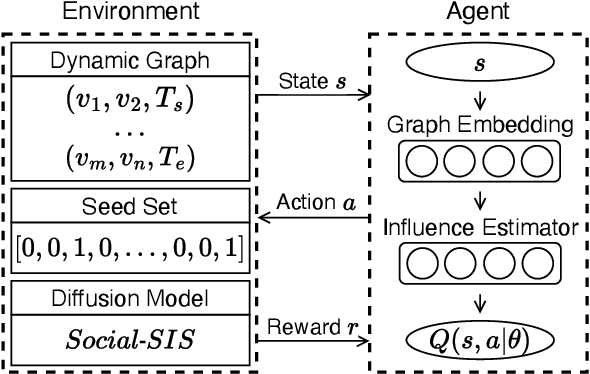
The influence maximization (IM) problem involves identifying a set of key individuals in a social network who can maximize the spread of influence through their network connections. With the advent of geometric deep learning on graphs, great progress has been made towards better solutions for the IM problem. In this paper, we focus on the dynamic non-progressive IM problem, which considers the dynamic nature of real-world social networks and the special case where the influence diffusion is non-progressive, i.e., nodes can be activated multiple times. We first extend an existing diffusion model to capture the non-progressive influence propagation in dynamic social networks. We then propose the method, DNIMRL, which employs deep reinforcement learning and dynamic graph embedding to solve the dynamic non-progressive IM problem. In particular, we propose a novel algorithm that effectively leverages graph embedding to capture the temporal changes of dynamic networks and seamlessly integrates with deep reinforcement learning. The experiments, on different types of real-world social network datasets, demonstrate that our method outperforms state-of-the-art baselines.

Reinforced Anytime Bottom Up Rule Learning for Knowledge Graph Completion

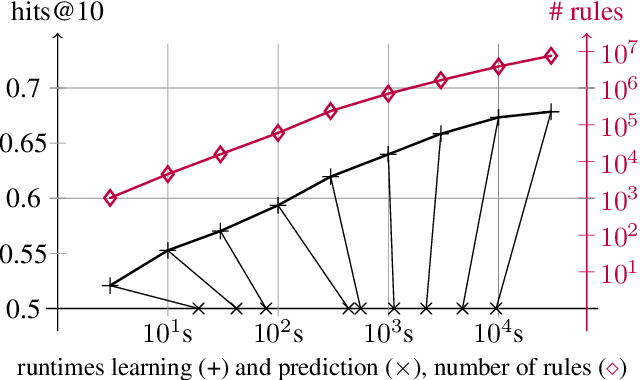
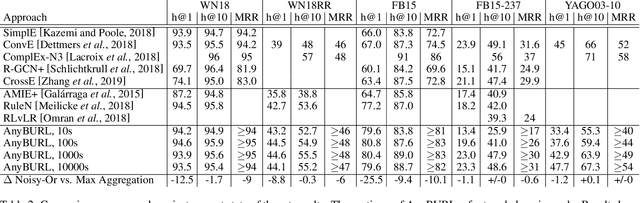
Most of todays work on knowledge graph completion is concerned with sub-symbolic approaches that focus on the concept of embedding a given graph in a low dimensional vector space. Against this trend, we propose an approach called AnyBURL that is rooted in the symbolic space. Its core algorithm is based on sampling paths, which are generalized into Horn rules. Previously published results show that the prediction quality of AnyBURL is on the same level as current state of the art with the additional benefit of offering an explanation for the predicted fact. In this paper, we are concerned with two extensions of AnyBURL. Firstly, we change AnyBURLs interpretation of rules from $\Theta$-subsumption into $\Theta$-subsumption under Object Identity. Secondly, we introduce reinforcement learning to better guide the sampling process. We found out that reinforcement learning helps finding more valuable rules earlier in the search process. We measure the impact of both extensions and compare the resulting approach with current state of the art approaches. Our results show that AnyBURL outperforms most sub-symbolic methods.

Towards Log-Linear Logics with Concrete Domains

We present $\mathcal{MEL}^{++}$ (M denotes Markov logic networks) an extension of the log-linear description logics $\mathcal{EL}^{++}$-LL with concrete domains, nominals, and instances. We use Markov logic networks (MLNs) in order to find the most probable, classified and coherent $\mathcal{EL}^{++}$ ontology from an $\mathcal{MEL}^{++}$ knowledge base. In particular, we develop a novel way to deal with concrete domains (also known as datatypes) by extending MLN's cutting plane inference (CPI) algorithm.