Reinforced Anytime Bottom Up Rule Learning for Knowledge Graph Completion
Paper and Code
Apr 09, 2020

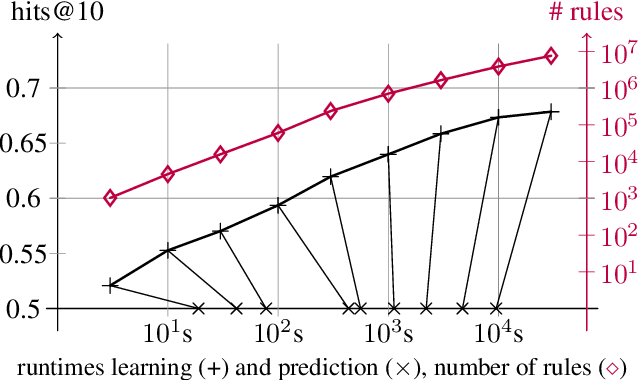
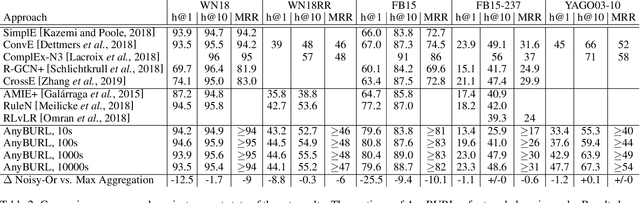
Most of todays work on knowledge graph completion is concerned with sub-symbolic approaches that focus on the concept of embedding a given graph in a low dimensional vector space. Against this trend, we propose an approach called AnyBURL that is rooted in the symbolic space. Its core algorithm is based on sampling paths, which are generalized into Horn rules. Previously published results show that the prediction quality of AnyBURL is on the same level as current state of the art with the additional benefit of offering an explanation for the predicted fact. In this paper, we are concerned with two extensions of AnyBURL. Firstly, we change AnyBURLs interpretation of rules from $\Theta$-subsumption into $\Theta$-subsumption under Object Identity. Secondly, we introduce reinforcement learning to better guide the sampling process. We found out that reinforcement learning helps finding more valuable rules earlier in the search process. We measure the impact of both extensions and compare the resulting approach with current state of the art approaches. Our results show that AnyBURL outperforms most sub-symbolic methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge