Meifang Zhu
Enhanced EADF for the Characterization of Large-Scale Antenna Arrays
Sep 23, 2022



Abstract:Massive multiple-input multiple-output (MIMO) is a key technique for fifth-generation (5G) and beyond communications. Therefore, accurate characterization of the responses of the large-scale antenna arrays at an arbitrary direction is critical. The effective aperture distribution function (EADF) can provide an analytic description of an antenna array based on a full-sphere measurement of the array in an anechoic chamber. However, as the aperture of an array becomes significantly larger, application of the EADF requires very dense spatial samples due to the large distance-offsets of the array elements to the reference point in the anechoic chamber. This leads to a prohibitive measurement time and a high computational complexity of EADF. In this paper, we first present the EADF applied to large-scale arrays, followed by an analytical analysis of the issue caused by the large array aperture. To solve this issue, an enhanced low-complexity EADF is proposed with a low complexity that is only considering the intrinsic characteristics of each array element rather than the aperture size of the array. Moreover, a measurement campaign conducted at the frequency band of 27-30\,GHz using a relatively large planar array is introduced, where the proposed enhanced EADF is applied and validated.
Beamspace Multidimensional ESPRIT Approaches for Simultaneous Localization and Communications
Nov 14, 2021
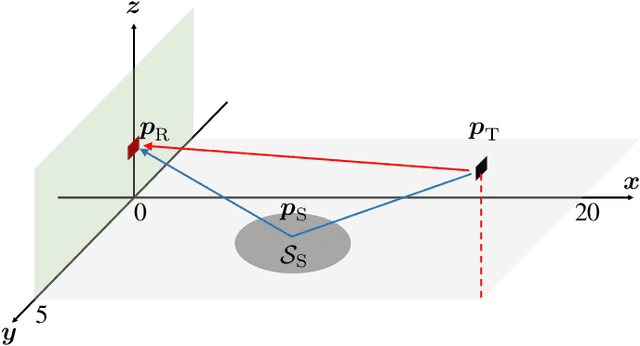

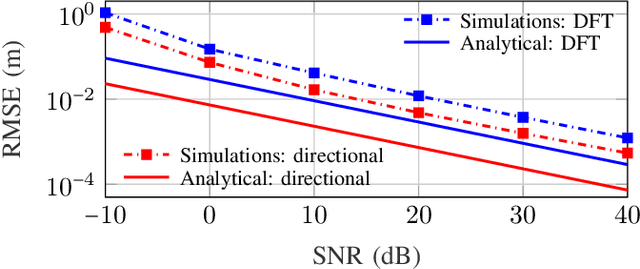
Abstract:Modern wireless communication systems operating at high carrier frequencies are characterized by a high dimensionality of the underlying parameter space (including channel gains, angles, delays, and possibly Doppler shifts). Estimating these parameters is valuable for communication purposes, but also for localization and sensing, making channel estimation a critical component in any joint communication and localization or sensing application. The high dimensionality make it difficult to use search-based methods such as maximum likelihood. Search-free methods such as ESPRIT provide an attractive alternative, but require a complex decomposition step in both the tensor and matrix version of ESPRIT. To mitigate this, we propose, develop, and analyze a reduced complexity beamspace ESPRIT method. Complexity is reduced both by beampace processing as well as low-complex implementation of the singular value decomposition. A novel perturbation analysis provides important insights for both channel estimation and localization performance. The proposed method is compared to the tensor ESPRIT method, in terms of channel estimation, communication, localization, and sensing performance, further validating the perturbation analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge